| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- SQL
- gcp
- dfs
- stratascratch
- 생성형AI
- LeetCode
- 파이썬
- 코드업
- Python3
- 파이썬알고리즘
- 슬라이딩윈도우
- Stack
- codeup
- GenerativeAI
- 릿코드
- 파이썬기초100제
- slidingwindow
- 알고리즘
- two-pointer
- tree
- nlp
- 니트코드
- 자연어처리
- 리트코드
- Python
- heap
- sql코테
- 투포인터
- GenAI
- medium
Archives
- Today
- Total
Tech for good
[Leetcode/Tree] 222. Count Complete Tree Nodes 본문
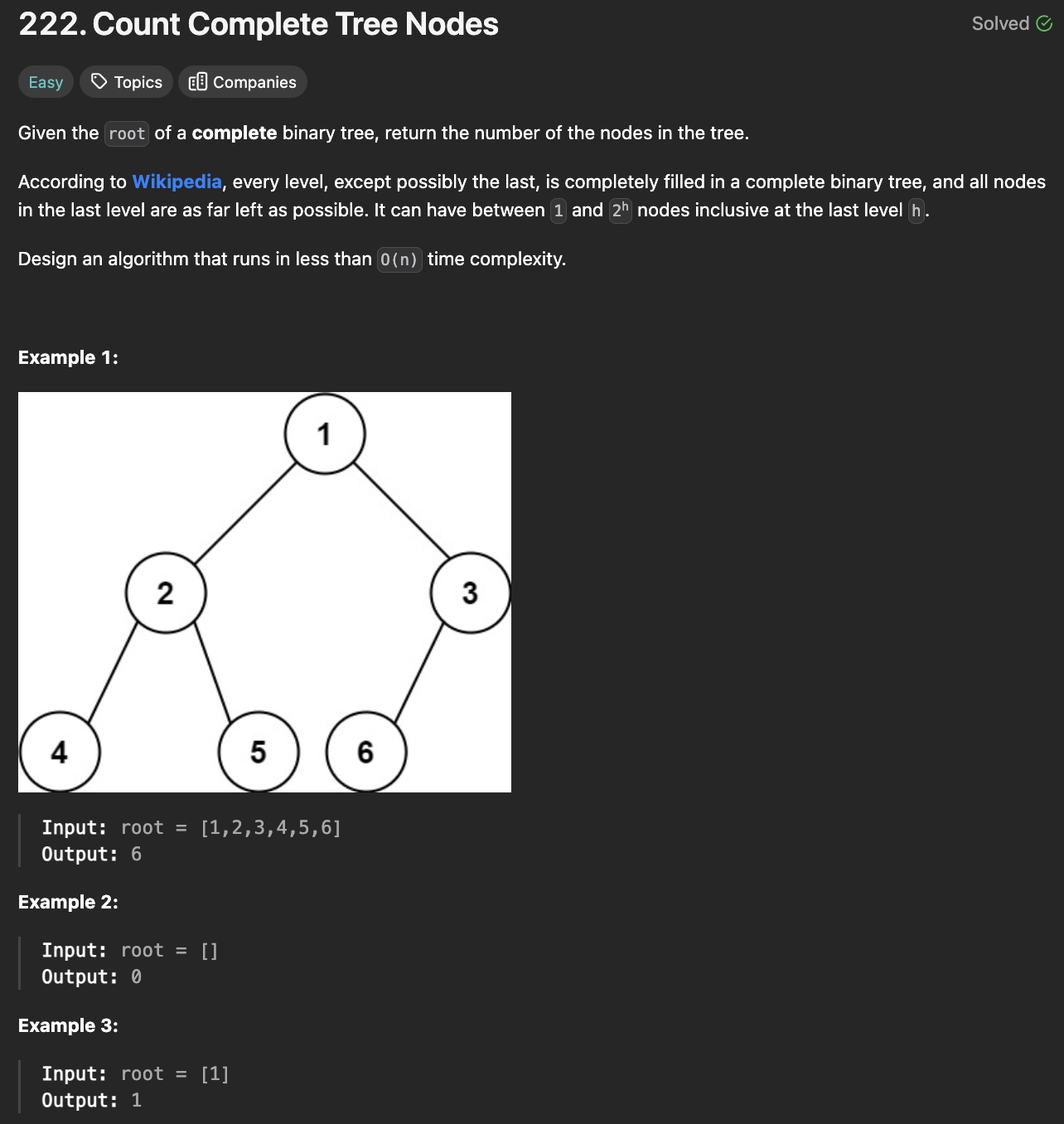


- 완전 이진 트리(Complete Binary Tree)의 노드 개수를 세는 문제이며, 최적화된 방법을 사용하여 O(n)보다 빠른 시간 복잡도로 해결해야 한다.
- 완전 이진 트리는 왼쪽부터 차곡차곡 채워지는 성질이 있기 때문에, 일반적인 트리 탐색(O(n))이 아니라, 이진 탐색을 활용한 O(log n * log n) 알고리즘을 사용할 수 있다.
- 완전 이진 트리는 모든 레벨이 가득 차 있으며, 마지막 레벨은 왼쪽부터 채워진 상태이다.
- 즉 왼쪽 서브트리의 높이와 오른쪽 서브트리의 높이가 같다면, 트리가 완전하게 채워진 형태라는 뜻이다.
- 다시 말해, 전체 노드 개수 == 꽉 찬 부분(완전한 트리) + 마지막 레벨의 노드 개수이다.
- 이렇게 노드가 모두 꽉 차 있는 완전 트리의 경우, 개수를 구하는 공식은 아래와 같다.

예제 분석


해결 방법 (O(log n * log n))
- 트리의 높이 계산
- 왼쪽 끝으로 내려가면서 트리의 높이(h)를 측정한다.
- 마지막 레벨의 노드 개수 탐색 (이진 탐색 사용)
- 마지막 레벨의 노드 개수는 0개에서 2^h - 1개 사이이다.
- 이를 이진 탐색을 사용하여 빠르게 찾는다.
- 전체 노드 개수 계산
- 노드 개수는 (2^h - 1) + 마지막 레벨의 노드 개수이다.
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def countNodes(self, root: Optional[TreeNode]) -> int:
if not root:
return 0 # 트리가 비어 있으면 0 반환
left, right = root.left, root.right # 왼쪽과 오른쪽 서브트리 초기화
left_height, right_height = 0, 0 # 왼쪽과 오른쪽 서브트리 높이 초기화
while left: # 왼쪽 끝까지 내려가면서 높이 구함
left_height += 1
left = left.left
while right: # 오른쪽 끝까지 내려가면서 높이 구함
right_height += 1
right = right.right
if left_height == right_height:
return (1 << (left_height + 1)) - 1 # 2^(h+1) - 1 (완전 이진 트리의 노드 개수 공식)
else:
return 1 + self.countNodes(root.left) + self.countNodes(root.right) # 루트 + 왼쪽 서브트리 + 오른쪽 서브트리📌 코드 설명
1️⃣ 왼쪽과 오른쪽 서브트리의 높이를 구함
- left_height는 왼쪽 끝까지 내려가며 높이를 증가.
- right_height는 오른쪽 끝까지 내려가며 높이를 증가.
2️⃣ 완전 이진 트리 여부 확인
- 왼쪽 높이 == 오른쪽 높이
→ 트리는 완전 이진 트리이므로 노드 개수 = (2^(h+1) - 1)
→ return (1 << (left_height + 1)) - 1
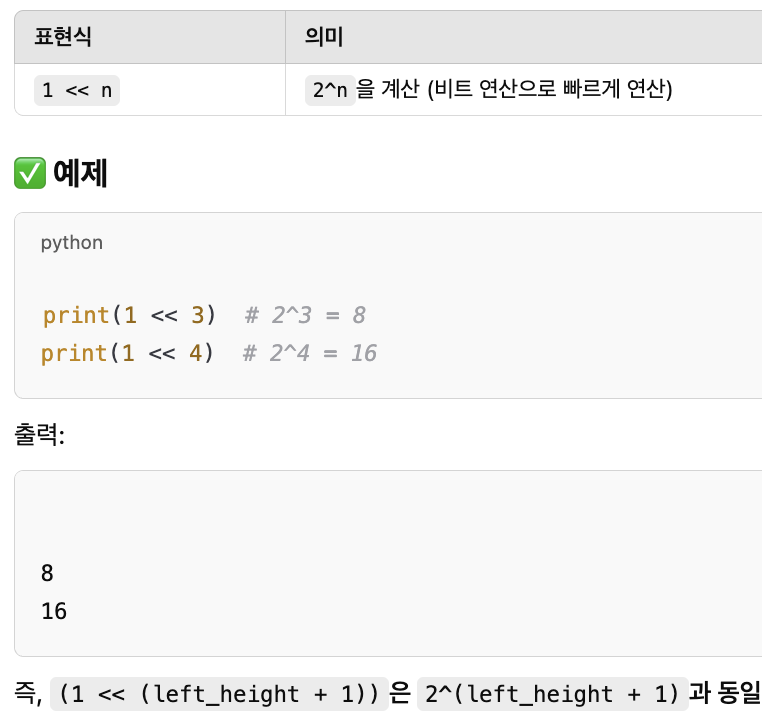
3️⃣ 왼쪽과 오른쪽 높이가 다를 경우
- 완전 이진 트리가 아니므로 일반적인 탐색 필요
→ 1 + self.countNodes(root.left) + self.countNodes(root.right)
'IT > Computer Science' 카테고리의 다른 글
| [Neetcode/Tree] Binary Tree Right Side View (0) | 2025.03.17 |
|---|---|
| [Leetcode/Tree] 617. Merge Two Binary Trees (0) | 2025.03.17 |
| [Neetcode/Tree] Binary Tree Level Order Traversal (0) | 2025.03.14 |
| [Leetcode/Tree] 501. Find Mode in Binary Search Tree (0) | 2025.03.14 |
| [Neetcode/Tree] Lowest Common Ancestor in Binary Search Tree (0) | 2025.03.12 |





