| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- heap
- Stack
- 자연어처리
- sql코테
- 알고리즘
- 릿코드
- Python3
- codeup
- 파이썬
- two-pointer
- stratascratch
- 니트코드
- GenerativeAI
- 슬라이딩윈도우
- SQL
- medium
- tree
- 생성형AI
- Python
- 코드업
- dfs
- 파이썬알고리즘
- 리트코드
- gcp
- 투포인터
- GenAI
- nlp
- LeetCode
- slidingwindow
- 파이썬기초100제
- Today
- Total
Tech for good
[T아카데미] 딥러닝을 활용한 자연어 처리 기술 실습 1강 본문
모든 출처: T아카데미(https://tacademy.skplanet.com/live/player/onlineLectureDetail.action?seq=123)
목차
1강. 딥러닝 및 자연어처리 소개
1.1. 자연어 이해 소개
1.2. Machine Learning Review
1.2.1. DNN 기본 Block 소개
1.3. Sequence to Sequence Learning
1.4. AI as Data transformation
1.4.1. Sequence Encoding
- Temporal Summarization
1.4.2. Sequence Decoding
[실습]
- 감성분석기 개발(N21 문제)
- 개체명 분석기 개발(N2N 문제)
- 대화모델 개발(N2M 문제)
1강. 딥러닝 및 자연어처리 소개
1.1. 자연어 이해 소개


강의에서 다룰 파트는 아래와 같다.

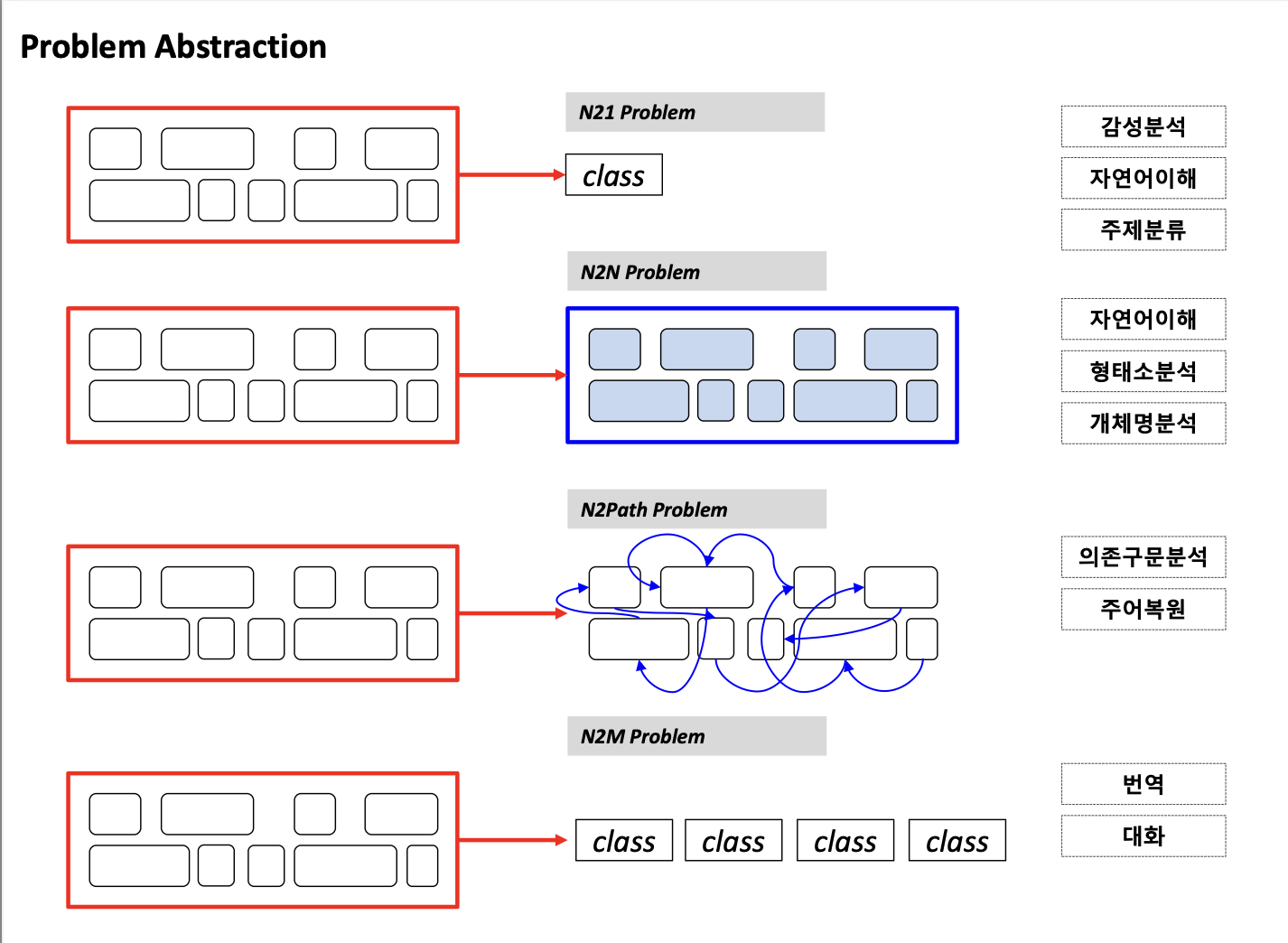
- 토큰 여러개가 전체의 input으로 들어올 때 -> 하나의 답(class)을 내놓는 문제 : N21 Problem
- 각 토큰을 다 보면서 각 토큰에 대응하는 답을 내놓는 문제 -> N2N Problem
- 토큰들을 보고 이 토큰들간의 그래프 관계를 뽑아내는 문제 : N2Path Problem
- input 토큰들이 N개이고, output 토큰들이 M개인 문제: N2M Problem

1.2. Machine Learning Review

이 강의는 Classification 문제 위주로 진행된다.
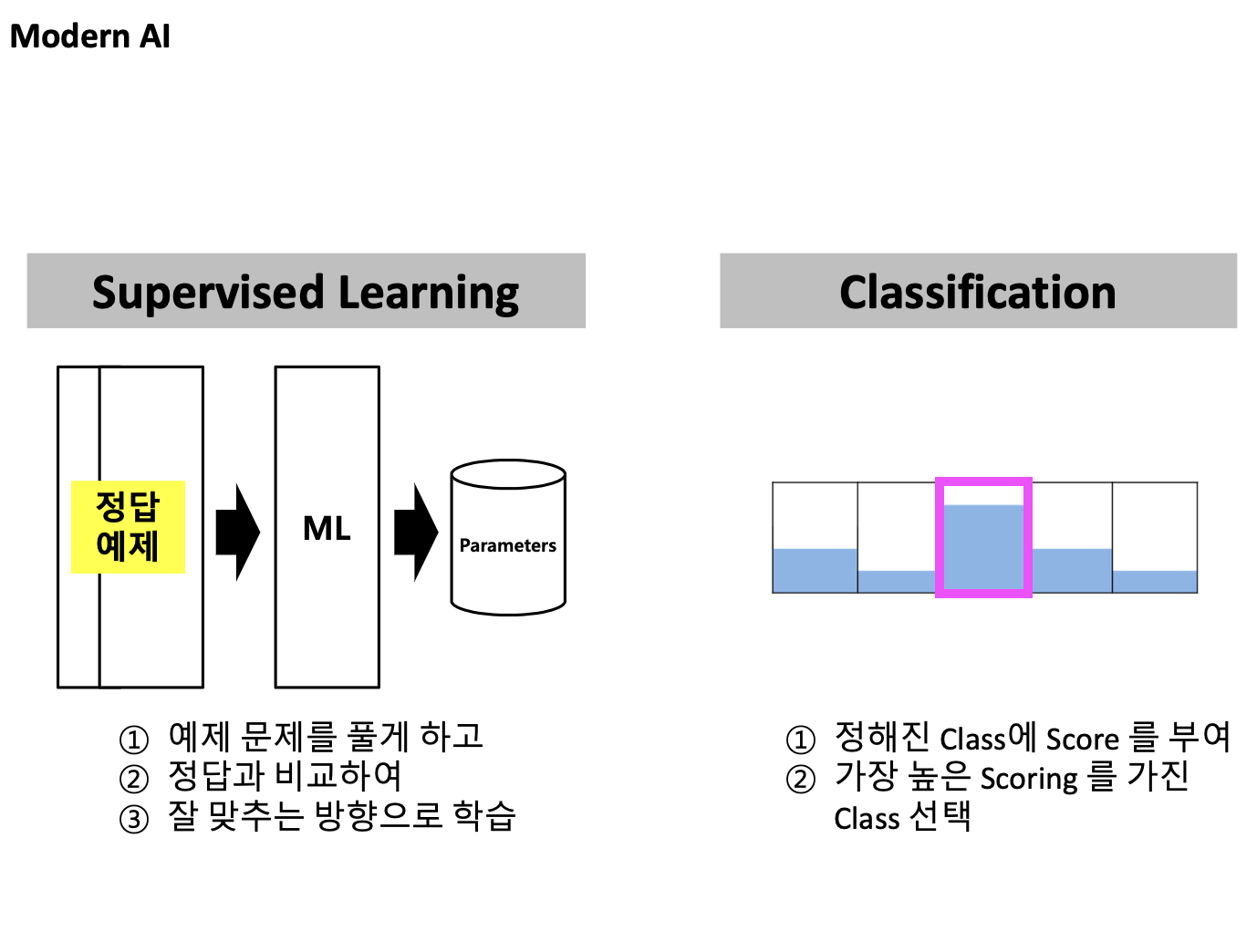
- Supervised Learning: 문제에 대한 정답을 주고 training 시키는 과정

모든 이해관계자들이 모여 class를 어떻게 설계할지 정해야한다.
1.2.1. DNN 기본 Block 소개



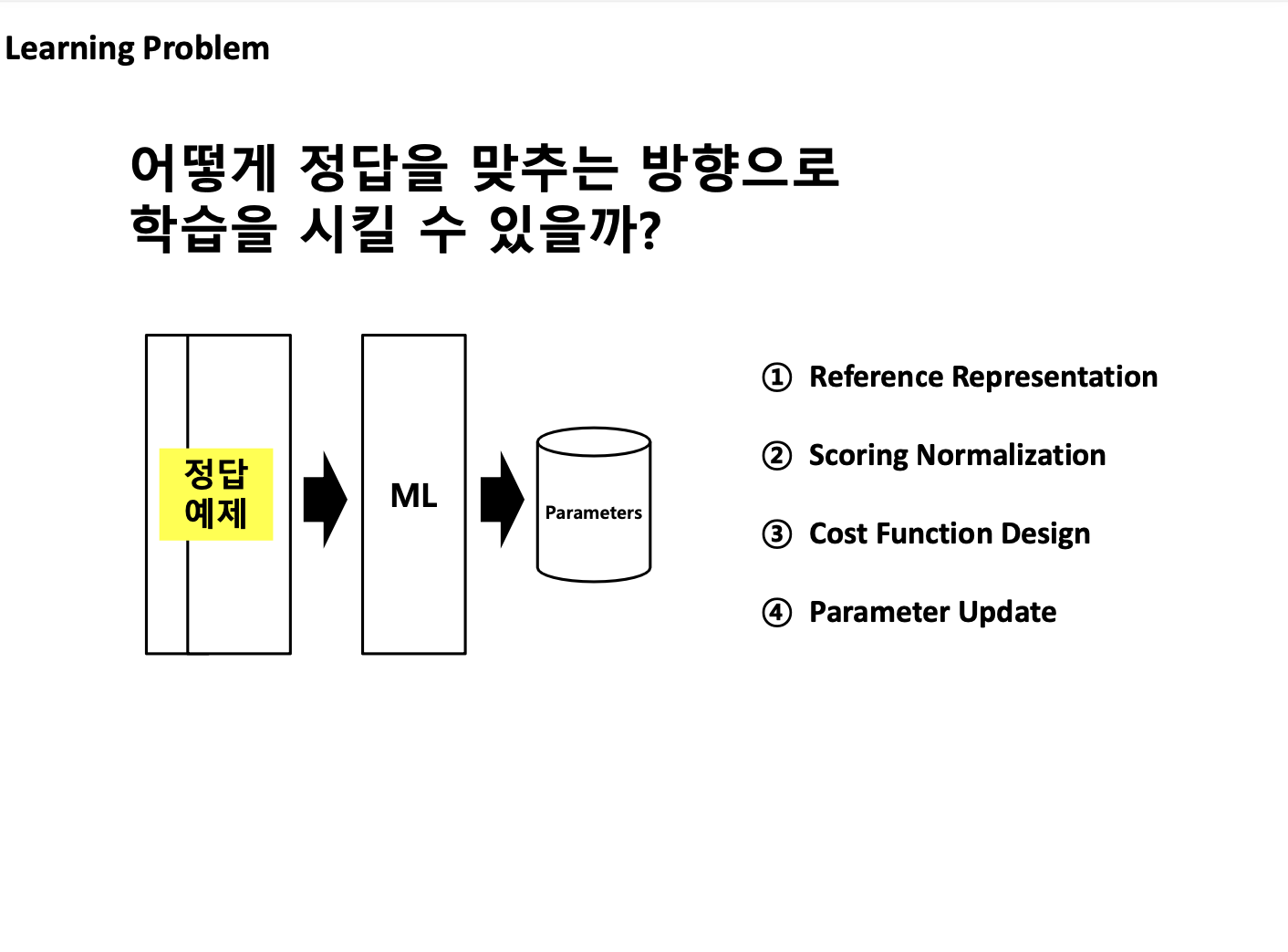
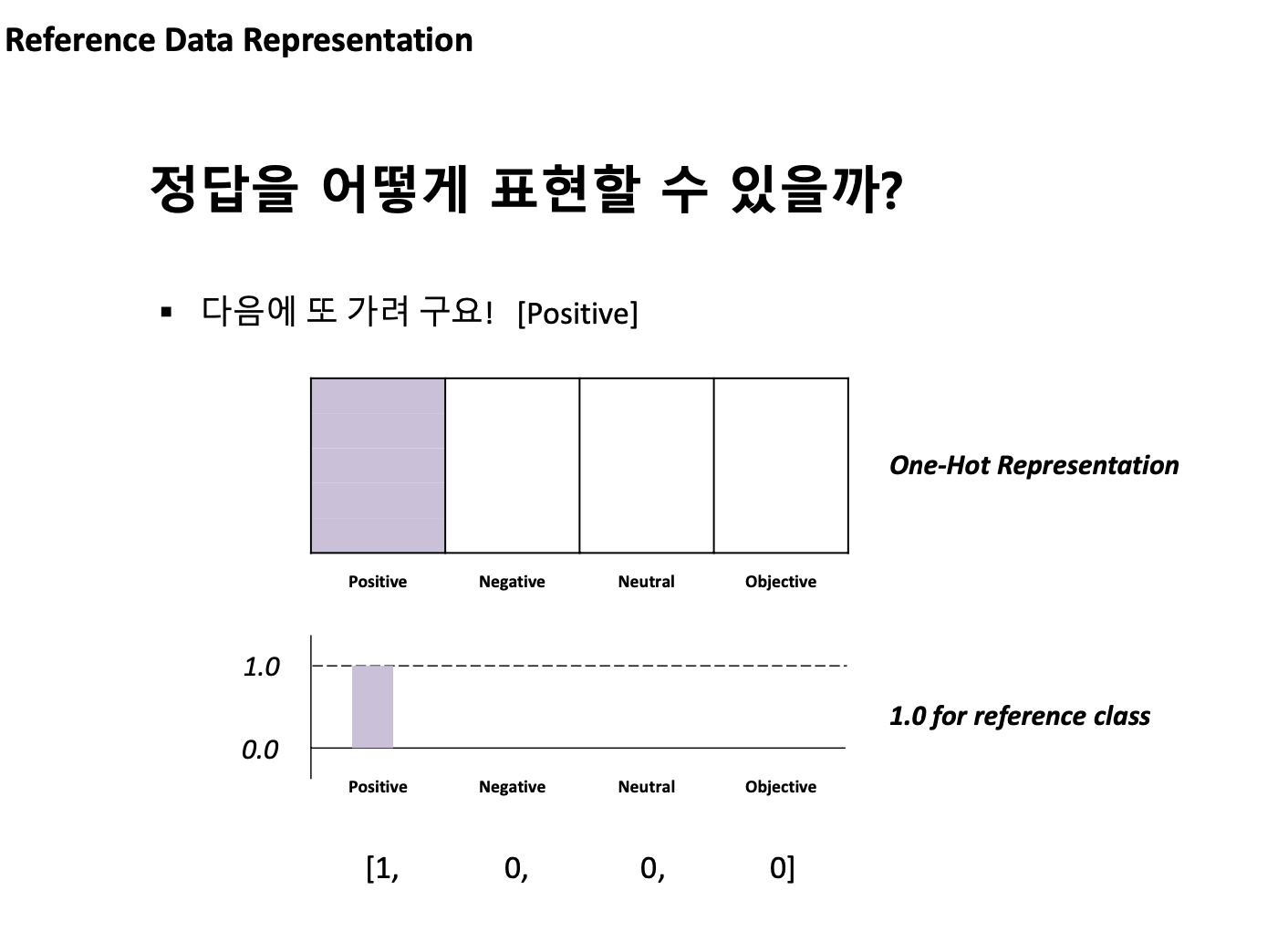
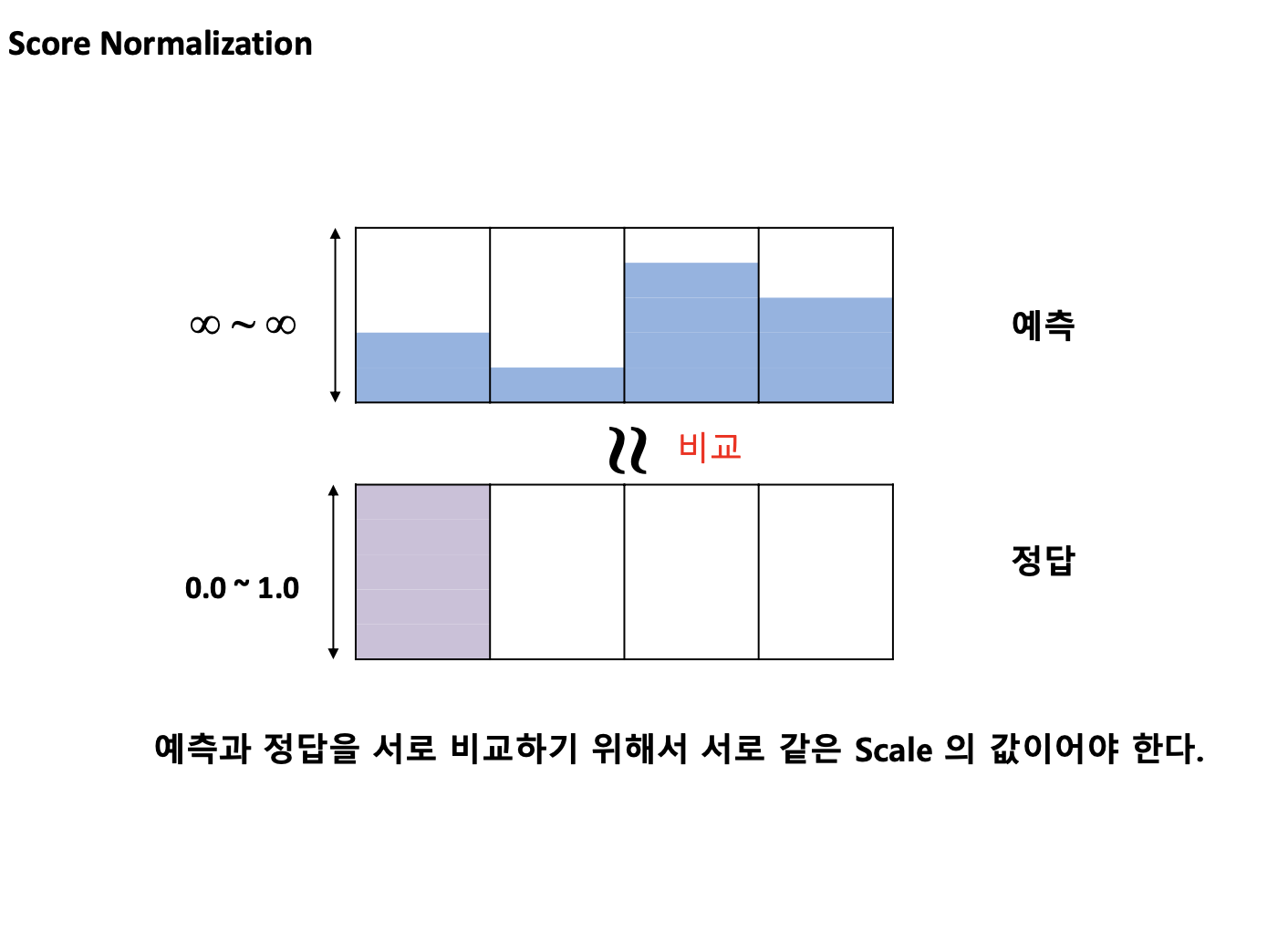
=> 예측값과 정답값을 비교하기 위해서는 스케일을 맞출 필요가 있다. 이 때 필요한 것이 아래에 나오는 softmax함수이다.


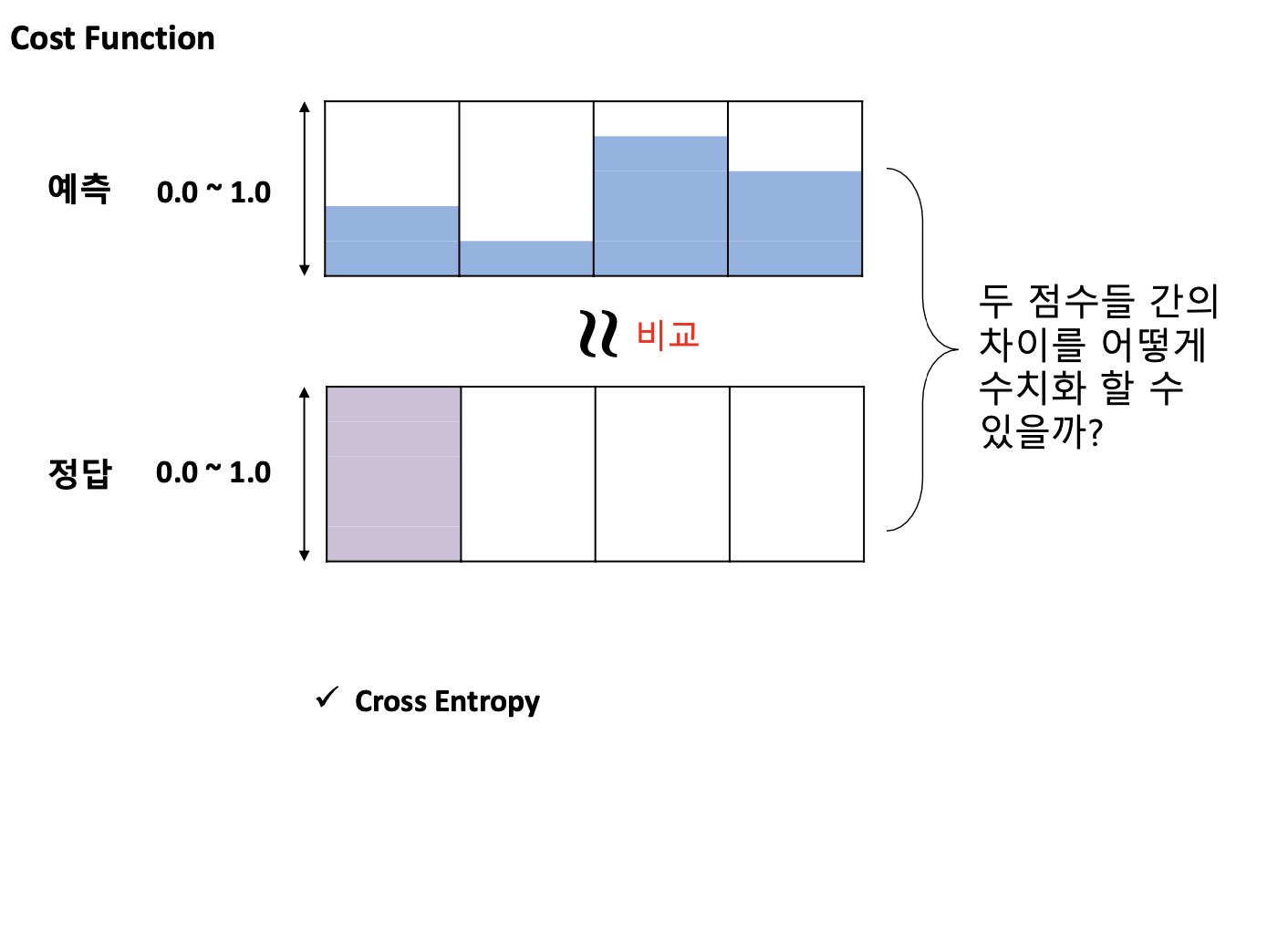
- Cross Entropy -> 두 확률분포 간의 차이를 계산해주는 방식
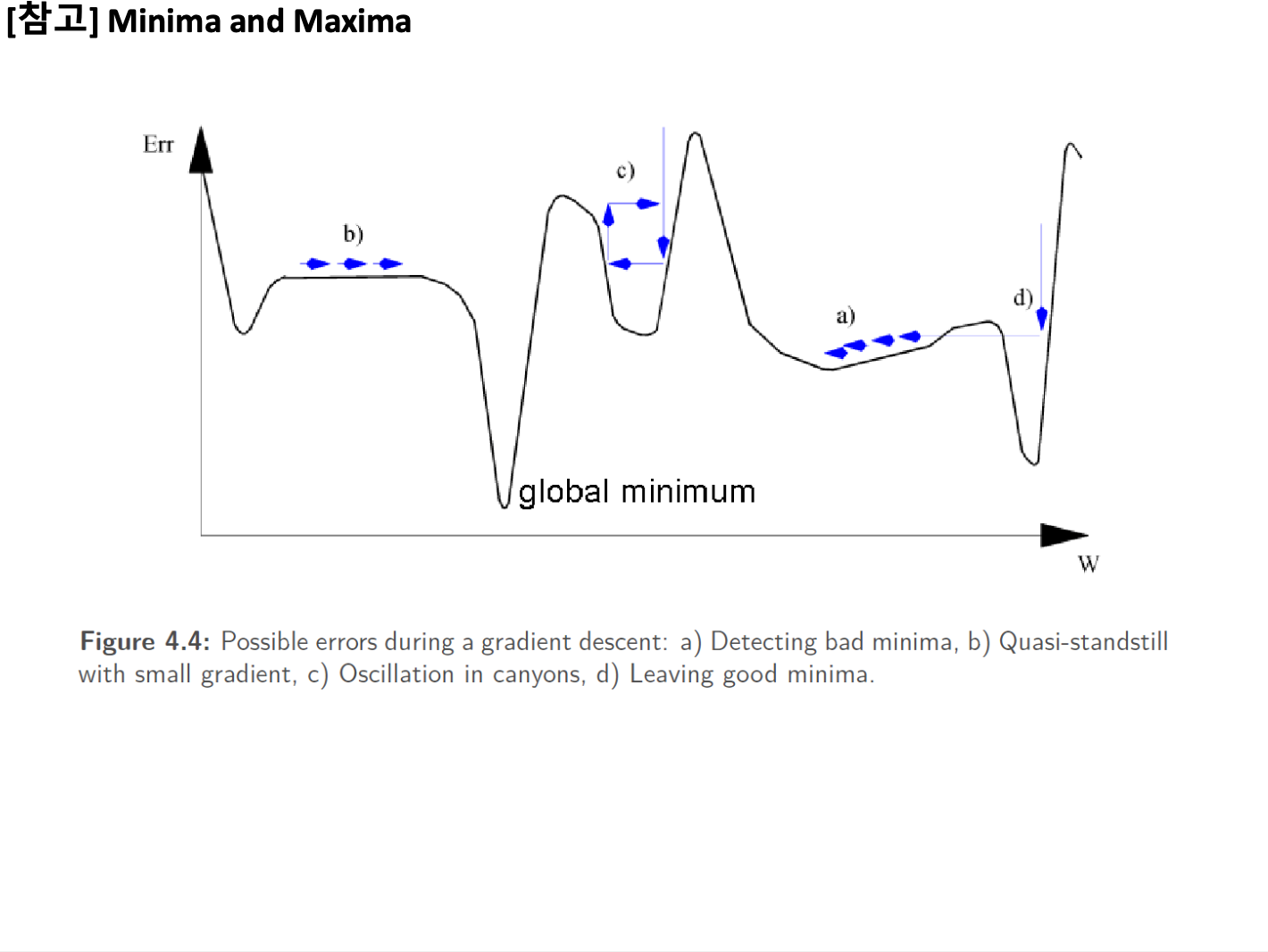
아래의 슬라이드는 그냥 참고용으로만 가볍게 볼 것!


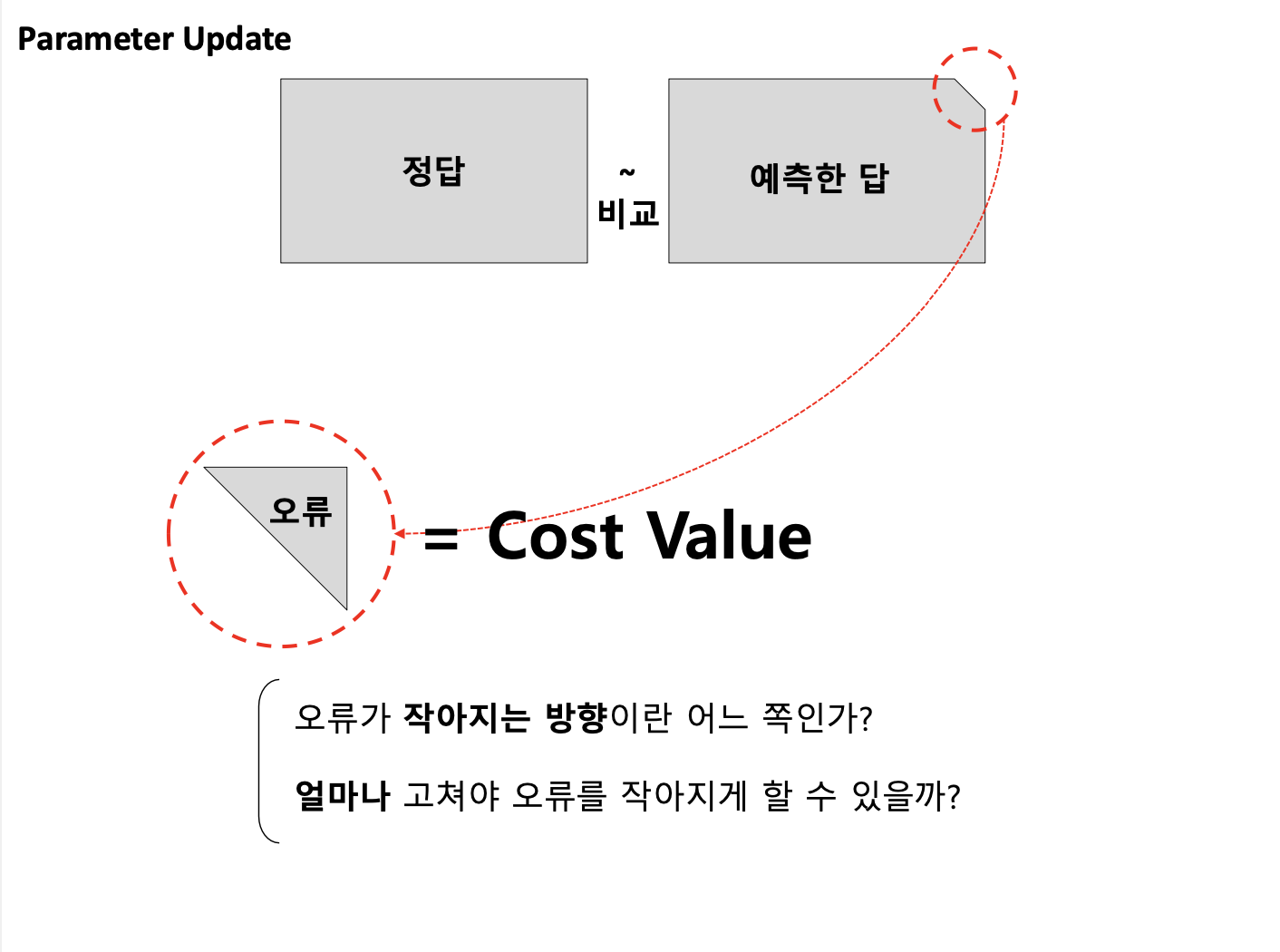


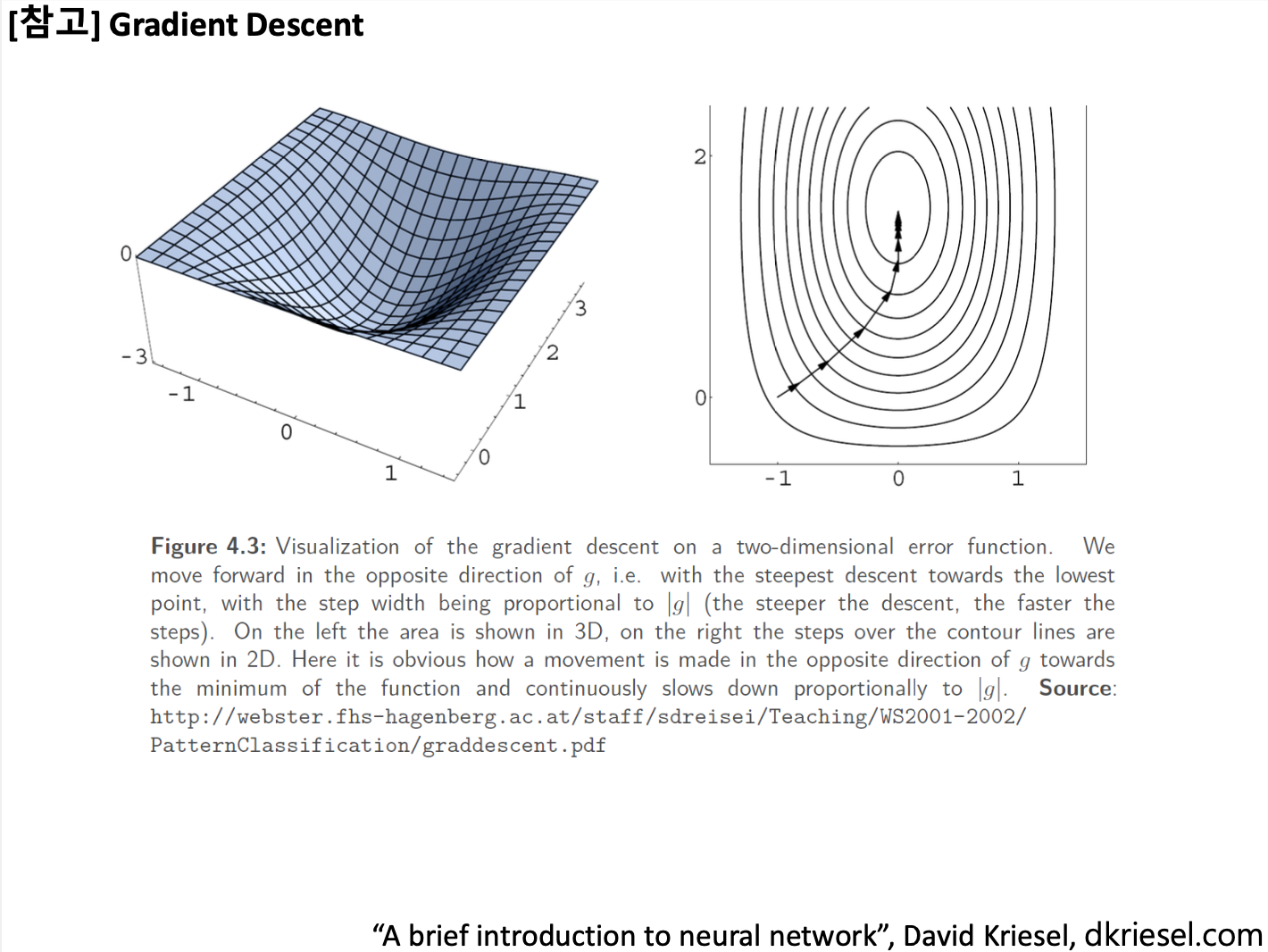
'파라미터 업데이트' or '학습 모델 갱신' or '학습' = 위치를 global minimum 혹은 local minimum하게 계속해서 바꿔가며 밑에까지 도달하게 만드는 것.
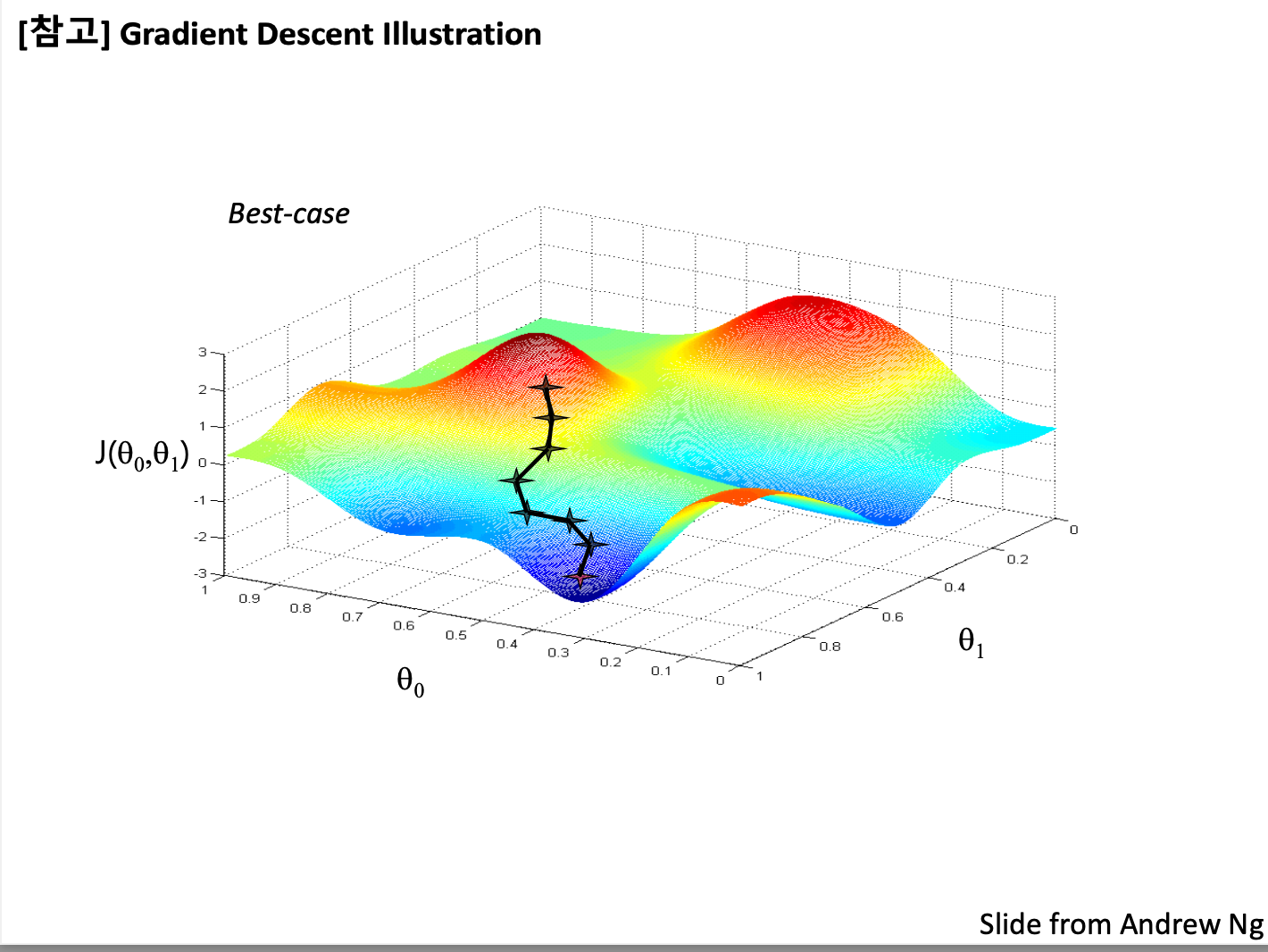
운이 좋으면 global minumum이 이렇게 밑에까지 잘 도달할 수 있지만,

운이 안좋으면, 밑에까지 도달(global minumum)하지 못하고 local minimum에 그치게 된다.


모든 점에 잘 적용되는 값 = 배치사이즈
e.g. 배치 사이즈가 3이면, 점 3개를 보고 그것을 잘 설명하는 선 하나를 찾는 것
+ 참고- 배치사이즈, 미니배치에 대한 설명이 잘 나와있는 블로그
https://welcome-to-dewy-world.tistory.com/86
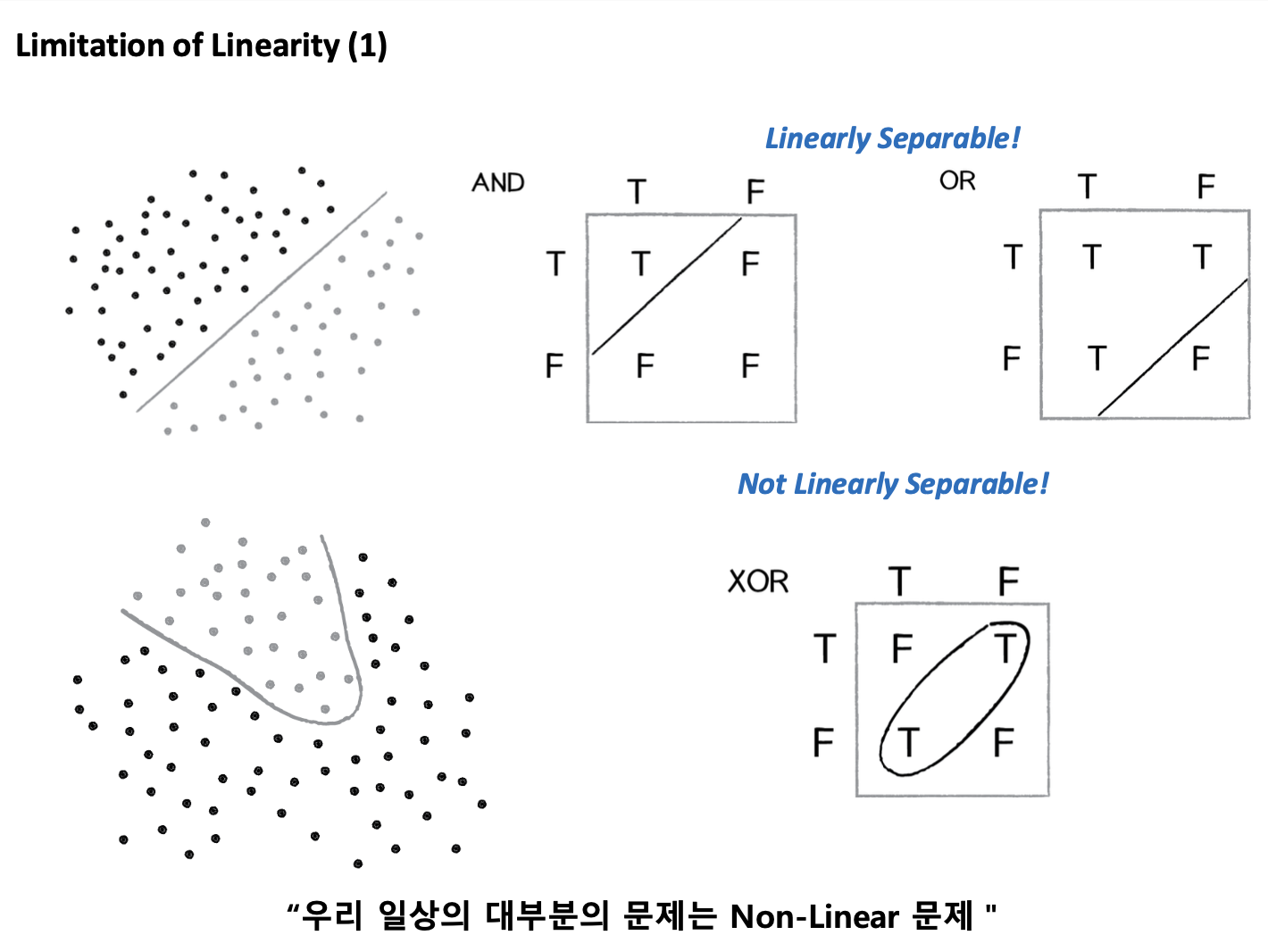
선을 긋는 문제(Linear 문제; Single layer perceptron)는 AND문제나 OR문제는 잘 풀 수 있다.
하지만 XOR 문제는 해결할 수 없다는 한계점이 있다.

위의 한계점을 보완하기 위해서는 Multi Layer를 만들어야 한다.

Multi-layer을 만들기 위해 단순히 Single Linear layer를 여러 개 합쳐서는 안된다.
오른쪽 그림과 같이 Non-linear activation function(e.g. RELU 함수)를 추가하여 Multi-layer를 만들어야 한다.
아래는 Non-linear activation function의 종류이다.
- sigmoid 함수
- tanh 함수
- ReLU 함수
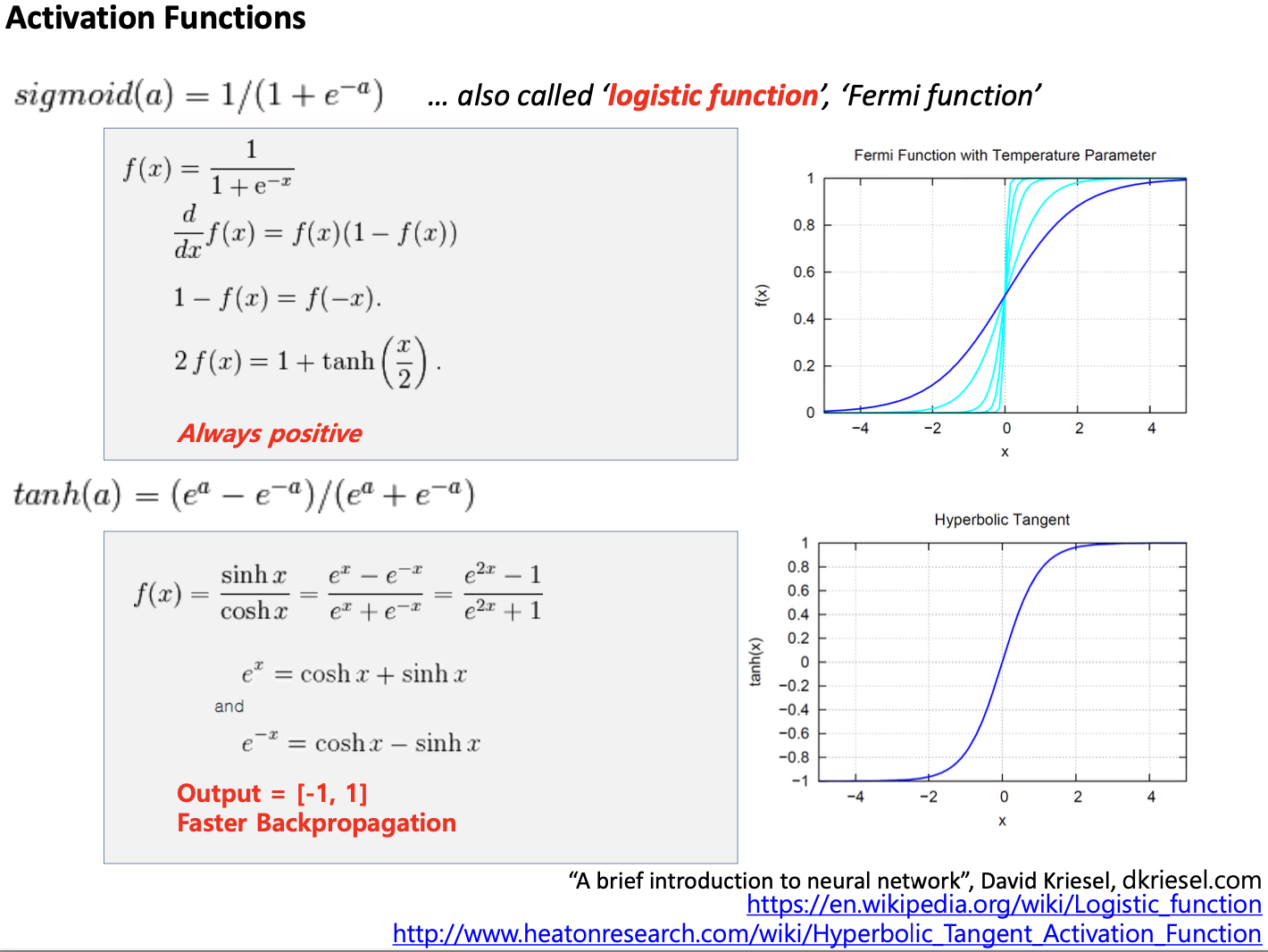
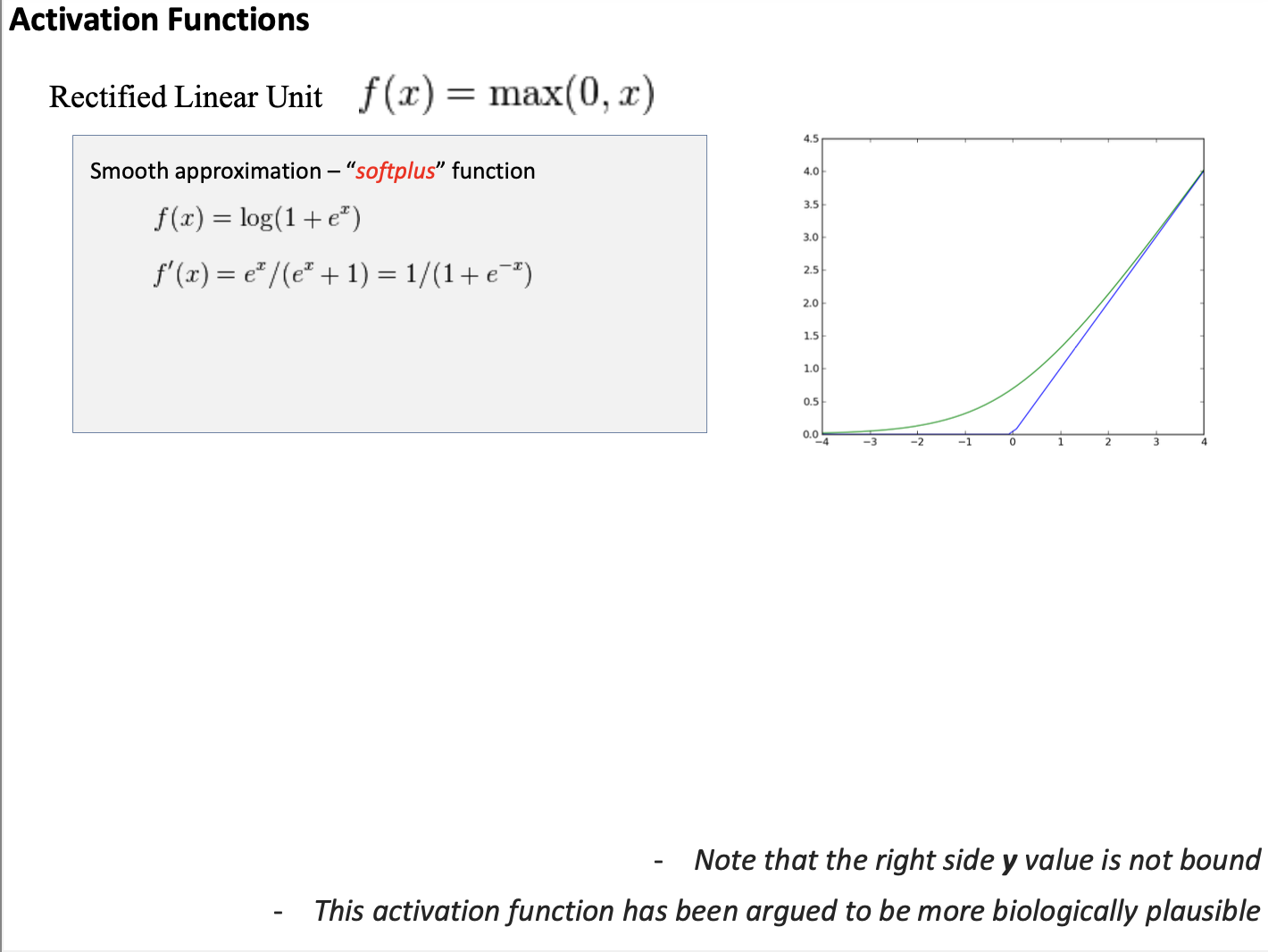
이 세가지 Non-linear 함수(sigmoid, tanh, ReLU)들은 모두 미분이 가능하다.


시그모이드 함수를 미분하면, 대부분이 0이다.
ReLU함수도 마찬가지로 미분을 하면, 왼쪽 부분이 0임을 알 수 있다.
즉, Backpropagation 과정에서 파라미터를 업데이트할 때 대부분의 값이 0이라는 것이다.
이는 non-linear function을 막 붙이게 될 경우, 값이 밑의 층까지 절대 내려오지 않는다는 것이다.
따라서 주의해서 잘 사용해야 한다.

딥러닝의 구조를 정리해보면 다음과 같다.
1. raw data를 숫자의 형태로 표현한다.
2. 숫자 형태로 표현된 값이 특정 레이어에 입력으로 들어가게 되고, 이 값들이 fully connected 형태로 계산된다.
3. fully connected로 계산된 값이 몇가지 activation function(Non-linear function)을 통해 다른 값으로 변형된다.
4. 변형된 최종 layer값과 정답값을 비교한다.
- Classification 문제의 경우 -> 비교척도로 Cross Entropy를 사용한다.
5. 계산된 값을 미분하여 Backpropagation 시켜준다.

전체적인 딥러닝의 구조
: Feed forward - Backpropagation - Feed forward - Backpropagation Feed forward - Backpropagation ...

'IT > Data Science' 카테고리의 다른 글
| <데이터 쓰기의 기술>, 차현나 (0) | 2021.08.27 |
|---|---|
| [처음 배우는 딥러닝 챗봇] Ch8. 챗봇 엔진 만들기 (0) | 2021.07.15 |
| [Colab] 구글 코랩 한글 폰트 깨짐 문제 해결하는 방법 (0) | 2021.06.01 |
| [Reading a thesis every week] Continual learning for named entity recognition(2021) (0) | 2021.05.30 |
| 자연어 언어모델 ‘BERT’ 2강 - 언어 모델(Language Model) | T아카데미 (0) | 2021.04.19 |


