| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- two-pointer
- 생성형AI
- 파이썬
- Python3
- 슬라이딩윈도우
- 투포인터
- SQL
- medium
- stratascratch
- 릿코드
- Greedy
- 파이썬알고리즘
- gcp
- heap
- GenerativeAI
- nlp
- slidingwindow
- GenAI
- 자연어처리
- 코드업
- array
- 니트코드
- codeup
- 리트코드
- LeetCode
- 파이썬기초100제
- dfs
- sql코테
- Python
- 알고리즘
- Today
- Total
Tech for good
[딥러닝을 이용한 자연어 처리 입문] 4. 카운트 기반의 단어 표현 - 4) TF-IDF(Term Frequency-Inverse Document Frequency) 본문
[딥러닝을 이용한 자연어 처리 입문] 4. 카운트 기반의 단어 표현 - 4) TF-IDF(Term Frequency-Inverse Document Frequency)
Diana Kang 2021. 10. 12. 18:05목차
4. 카운트 기반의 단어 표현(Count based word Representation)
4.4. TF-IDF(Term Frequency-Inverse Document Frequency)
4.4.1. TF-IDF(단어 빈도-역 문서 빈도, Term Frequency-Inverse Document Frequency)
(1) tf(d,t) : 특정 문서 d에서의 특정 단어 t의 등장 횟수
(2) df(t) : 특정 단어 t가 등장한 문서의 수
(3) idf(d,t) : df(t)에 반비례하는 수
4.4.2. 파이썬으로 TF-IDF 직접 구현하기
4.4.3. 사이킷런을 이용한 DTM과 TF-IDF 실습
4. 카운트 기반의 단어 표현
4.4. TF-IDF(Term Frequency-Inverse Document Frequency)
이번 챕터에서는 DTM 내에 있는 각 단어에 대한 중요도를 계산할 수 있는 TF-IDF 가중치에 대해 알아보도록 한다. TF-IDF를 사용하면 기존의 DTM을 사용하는 것보다 더 많은 정보를 고려하여 문서들을 비교할 수 있다. (주의할 점은 TF-IDF가 항상 DTM보다 성능이 뛰어나진 않는다.)
4.4.1. TF-IDF(단어 빈도-역 문서 빈도, Term Frequency-Inverse Document Frequency)
TF-IDF(Term Frequency-Inverse Document Frequency)는 단어의 빈도와 역 문서 빈도(문서의 빈도에 특정 식을 취함)를 사용하여 DTM 내의 각 단어들마다 중요한 정도를 가중치로 주는 방법이다. 사용 방법은 우선 DTM을 만든 후, TF-IDF 가중치를 부여한다.
TF-IDF는 주로 문서의 유사도를 구하는 작업, 검색 시스템에서 검색 결과의 중요도 를 정하는 작업, 문서 내에서 특정 단어의 중요도 를 구하는 작업 등에 쓰일 수 있다.
TF-IDF는 TF와 IDF를 곱한 값을 의미하는데 이를 식으로 표현해보겠다. 문서를 d, 단어를 t, 문서의 총 개수를 n이라고 표현할 때 TF, DF, IDF는 각각 다음과 같이 정의할 수 있다.
(1) tf(d,t) : 특정 문서 d에서의 특정 단어 t의 등장 횟수
TF는 앞에서 배운 DTM에서 각 단어들이 가진 값들입니다. (DTM은 각 문서에서의 각 단어의 등장 빈도를 나타내는 값이다.)
(2) df(t) : 특정 단어 t가 등장한 문서의 수
여기서는 특정 단어가 각 문서, 또는 문서들에서 몇 번 등장했는지는 관심갖지 않으며 오직 특정 단어 t가 등장한 문서의 수에만 관심을 가진다. 앞서 배운 DTM에서 바나나는 문서2와 문서3에서 등장했다. 이 경우, 바나나의 df는 2이다. 문서3에서 바나나가 두 번 등장했지만, 그것은 중요한 게 아니다. 심지어 바나나란 단어가 문서2에서 100번 등장했고, 문서3에서 200번 등장했다고 하더라도 바나나의 df는 2가 된다.
(3) idf(d,t) : df(t)에 반비례하는 수

IDF라는 이름을 보고 DF의 역수가 아닐까 생각했다면, IDF는 DF의 역수를 취하고 싶은 것은 맞다. 다만 log와 분모에 1을 더해주게 된다. 그 이유는 log를 사용하지 않았을 때, IDF를 DF의 역수(n/df(t)라는 식)로 사용한다면 총 문서의 수 n이 커질 수록, IDF의 값은 기하급수적으로 커지기 때문이다. 그렇기 때문에 log를 사용해야 한다.
왜 log가 필요한지 n=1,000,000일 때의 예를 들어보자. log의 밑은 10을 사용한다고 가정하였을 때 결과는 아래와 같다.

그렇다면 log를 사용하지 않으면 idf의 값이 어떻게 커지는지 살펴보자.

또 다른 직관적인 설명은 불용어 등과 같이 자주 쓰이는 단어들은 비교적 자주 쓰이지 않는 단어들보다 최소 수십 배 자주 등장한다. 그런데 비교적 자주 쓰이지 않는 단어들조차 희귀 단어들과 비교하면 또 최소 수백 배는 더 자주 등장하는 편이다. 이 때문에 log를 씌워주지 않으면, 희귀 단어들에 엄청난 가중치가 부여될 수 있다. 로그를 씌우면 이런 격차를 줄이는 효과가 있다.
또한 log 안의 식에서 분모에 1을 더해주는 이유는 첫번째 이유로는 특정 단어가 전체 문서에서 등장하지 않을 경우에 분모가 0이 되는 상황을 방지하기 위함이다.
TF-IDF는 모든 문서에서 자주 등장하는 단어는 중요도가 낮다고 판단하며, 특정 문서에서만 자주 등장하는 단어는 중요도가 높다고 판단한다. TF-IDF 값이 낮으면 중요도가 낮은 것이며, TF-IDF 값이 크면 중요도가 큰 것이다. 즉, the나 a와 같이 불용어의 경우에는 모든 문서에 자주 등장하기 마련이기 때문에 자연스럽게 불용어의 TF-IDF의 값은 다른 단어의 TF-IDF에 비해서 낮아지게 된다.

앞서 DTM을 설명하기위해 들었던 위의 예제를 가지고 TF-IDF에 대해 이해해보자. 우선 TF는 앞서 사용한 DTM을 그대로 사용하면 된다. 그것이 각 문서 단어의 TF가 되기 때문이다.
그렇다면 이제 구해야할 것은 TF와 곱해야할 값인 IDF이다. 로그는 자연 로그를 사용할 것이다. 자연 로그는 로그의 밑을 자연 상수 e(e=2.718281...)를 사용하는 로그를 말한다. IDF 계산을 위해 사용하는 로그의 밑은 TF-IDF를 사용하는 사용자가 임의로 정할 수 있는데, 여기서 로그는 마치 기존의 값에 곱하여 값의 크기를 조절하는 상수의 역할을 한다. 보통 각종 프로그래밍 언어나 프로그램에서 패키지로 지원하는 TF-IDF의 로그는 대부분 자연 로그를 사용한다. 이는 log라고 표현하지 않고, ln이라고 표현한다.

문서의 총 수는 4이기 때문에 ln 안에서 분자는 늘 4으로 동일하다. 분모의 경우에는 각 단어가 등장한 문서의 수(DF)를 의미하는데, 예를 들어서 '먹고'의 경우에는 총 2개의 문서(문서1, 문서2)에 등장했기 때문에 2라는 값을 가진다. 각 단어에 대해서 IDF의 값을 비교해보면 문서 1개에만 등장한 단어와 문서2개에만 등장한 단어는 값의 차이를 보인다. IDF는 여러 문서에서 등장한 단어의 가중치를 낮추는 역할을 하기 때문이다.
그러면 이제 TF-IDF를 계산해보도록 하겠다. TF가 DTM을 그대로 가져오면 문서-단어의 TF를 가져오는 것이기 때문에 앞서 사용한 DTM에서 단어 별로 위의 IDF값을 그대로 곱해주기만 하면 TF-IDF가 나오게 된다.

사실 예제 문서가 굉장히 간단하기 때문에 계산은 매우 쉽다. 문서3에서의 바나나만 TF 값이 2이므로 IDF에 2를 곱해주고, 나머진 TF 값이 1이므로 그대로 IDF 값을 가져오면 된다. 문서2에서의 바나나의 TF-IDF 가중치와 문서3에서의 바나나의 TF-IDF 가중치가 다른 것을 볼 수 있다. 수식적으로 말하면, TF가 각각 1과 2로 달랐기 때문인데 TF-IDF에서의 관점에서 보자면 TF-IDF는 특정 문서에서 자주 등장하는 단어는 그 문서 내에서 중요한 단어로 판단하기 때문이다. 문서2에서는 바나나를 한 번 언급했지만, 문서3에서는 바나나를 두 번 언급했기 때문에 문서3에서의 바나나를 더욱 중요한 단어라고 판단하는 것이다.
4.4.2. 파이썬으로 TF-IDF 직접 구현하기
위의 계산 과정을 파이썬으로 직접 구현해보자. 우선 필요한 도구들을 임포트한다.
import pandas as pd # 데이터프레임 사용을 위해
from math import log # IDF 계산을 위해앞의 설명에서 사용한 4개의 문서를 docs에 저장한다.
docs = [
'먹고 싶은 사과',
'먹고 싶은 바나나',
'길고 노란 바나나 바나나',
'저는 과일이 좋아요'
]
vocab = list(set(w for doc in docs for w in doc.split()))
vocab.sort()TF, IDF, 그리고 TF-IDF 값을 구하는 함수를 구현한다.
N = len(docs) # 총 문서의 수
def tf(t, d):
return d.count(t)
def idf(t):
df = 0
for doc in docs:
df += t in doc
return log(N/(df + 1))
def tfidf(t, d):
return tf(t,d)* idf(t)이제 TF를 구할 것이다. 다시 말해 DTM을 데이터프레임에 저장하여 출력해보자.
result = []
for i in range(N): # 각 문서에 대해서 아래 명령을 수행
result.append([])
d = docs[i]
for j in range(len(vocab)):
t = vocab[j]
result[-1].append(tf(t, d))
tf_ = pd.DataFrame(result, columns = vocab)
tf_
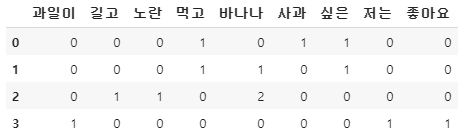
정상적으로 DTM이 출력되었다. 이제 각 단어에 대한 IDF 값을 구해보자.
result = []
for j in range(len(vocab)):
t = vocab[j]
result.append(idf(t))
idf_ = pd.DataFrame(result, index = vocab, columns = ["IDF"])
idf_
위에서 수기로 구한 IDF 값들과 정확히 일치한다. 이제 TF-IDF 행렬을 출력해보자.
result = []
for i in range(N):
result.append([])
d = docs[i]
for j in range(len(vocab)):
t = vocab[j]
result[-1].append(tfidf(t,d))
tfidf_ = pd.DataFrame(result, columns = vocab)
tfidf_
지금까지 TF-IDF의 가장 기본적인 식에 대해서 학습하고, 이를 실제로 구현하는 실습을 진행해보았다. 그런데 사실 실제 TF-IDF 구현을 제공하고 있는 많은 패키지들은 패키지마다 식이 조금씩 다르긴 하지만, 위에서 배운 기본 식에서 조정된 식을 사용한다. 그 이유는 위의 기본적인 식을 바탕으로 한 구현에도 여전히 문제점이 존재하기 때문이다. 만약 전체 문서의 수 n이 4인데, df(t)의 값이 3인 경우에는 어떤 일이 벌어질까? df(t)에 1이 더해지면서 log항의 분자와 분모의 값이 같아지게 된다.
이는 log의 진수값이 1이 되면서 idf(d,t)의 값이 0이 됨을 의미한다. 식으로 표현하면 idf(d,t)=log(n/(df(t)+1))=0이다. IDF의 값이 0이라면 더 이상 가중치의 역할을 수행하지 못한다. 그래서 실제 구현체는 idf(d,t)=log(n/(df(t)+1))+1과 같이 log항에 1을 더해줘서 log항의 값이 0이 되더라도 IDF가 최소 1이상의 값을 가지도록 한다. 사이킷런도 이 방식을 사용하여 구현한다.
4.4.3. 사이킷런을 이용한 DTM과 TF-IDF 실습
사이킷런을 통해 DTM과 TF-IDF를 만들어보겠다. BoW 챕터에서 배운 CountVectorizer를 사용하면 DTM을 만들 수 있다.
from sklearn.feature_extraction.text import CountVectorizer
corpus = [
'you know I want your love',
'I like you',
'what should I do ',
]
vector = CountVectorizer()
print(vector.fit_transform(corpus).toarray()) # 코퍼스로부터 각 단어의 빈도 수를 기록한다.
print(vector.vocabulary_) # 각 단어의 인덱스가 어떻게 부여되었는지를 보여준다.[[0 1 0 1 0 1 0 1 1]
[0 0 1 0 0 0 0 1 0]
[1 0 0 0 1 0 1 0 0]]
{'you': 7, 'know': 1, 'want': 5, 'your': 8, 'love': 3, 'like': 2, 'what': 6, 'should': 4, 'do': 0}
DTM이 완성되었다. DTM에서 각 단어의 인덱스가 어떻게 부여되었는지를 확인하기 위해 인덱스를 확인해보았다. 첫번째 열의 경우에는 0의 인덱스를 가진 do이다. do는 세번째 문서에만 등장했기 때문에, 세번째 행에서만 1의 값을 가진다. 두번째 열의 경우에는 1의 인덱스를 가진 know이다. know는 첫번째 문서에만 등장했기 때문에 첫번째 행에서만 1의 값을 가진다.
사이킷런은 TF-IDF를 자동 계산해주는 TfidfVectorizer를 제공한다. 향후 실습을 하다가 혼란이 생기지 않도록 언급하자면, 사이킷런의 TF-IDF는 위에서 배웠던 보편적인 TF-IDF 식에서 좀 더 조정된 다른 식을 사용한다. 하지만 크게 다른 식은 아니며(IDF의 로그항의 분자에 1을 더해주며, 로그항에 1을 더해주고, TF-IDF에 L2 정규화라는 방법으로 값을 조정하는 등의 차이), 여전히 TF-IDF가 가진 의도를 그대로 갖고 있으므로 사이킷런의 TF-IDF를 그대로 사용해도 좋다.
from sklearn.feature_extraction.text import TfidfVectorizer
corpus = [
'you know I want your love',
'I like you',
'what should I do ',
]
tfidfv = TfidfVectorizer().fit(corpus)
print(tfidfv.transform(corpus).toarray())
print(tfidfv.vocabulary_)[[0. 0.46735098 0. 0.46735098 0. 0.46735098 0. 0.35543247 0.46735098]
[0. 0. 0.79596054 0. 0. 0. 0. 0.60534851 0. ]
[0.57735027 0. 0. 0. 0.57735027 0. 0.57735027 0. 0. ]]
{'you': 7, 'know': 1, 'want': 5, 'your': 8, 'love': 3, 'like': 2, 'what': 6, 'should': 4, 'do': 0}
이제 BoW, DTM, TF-IDF에 대해서 전부 학습했다. 문서들 간의 유사도를 구하기 위한 재료 손질하는 방법을 배운 셈이다. 케라스로도 DTM과 TF-IDF 행렬을 만들 수 있는데, 이는 다층 퍼셉트론으로 텍스트 분류하기 챕터에서 별도로 다루겠다. 이제 다음 챕터에서 유사도를 구하는 방법을 학습한 후 실습을 진행한다.




