| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 알고리즘
- two-pointer
- nlp
- gcp
- 투포인터
- 구글퀵랩
- GenerativeAI
- Python3
- heap
- 슬라이딩윈도우
- 파이썬
- Microsoft
- 니트코드
- GenAI
- 리트코드
- 파이썬기초100제
- 코드업
- slidingwindow
- stratascratch
- medium
- dfs
- codeup
- 자연어처리
- Python
- 생성형AI
- 파이썬알고리즘
- 릿코드
- SQL
- sql코테
- LeetCode
- Today
- Total
Tech for good
[딥러닝을 이용한 자연어 처리 입문] 6. 토픽 모델링(Topic Modeling)- 1) 잠재 의미 분석(Latent Semantic Analysis, LSA) 본문
[딥러닝을 이용한 자연어 처리 입문] 6. 토픽 모델링(Topic Modeling)- 1) 잠재 의미 분석(Latent Semantic Analysis, LSA)
Diana Kang 2021. 10. 14. 09:45목차
6. 토픽 모델링(Topic Modeling)
6.1. 잠재 의미 분석(Latent Semantic Analysis; LSA)
6.1.1. 특이값 분해(Singular Value Decomposition, SVD)
(1) 전치 행렬(Transposed Matrix)
(2) 단위 행렬(Identity Matrix)
(3) 역행렬(Inverse Matrix)
(4) 직교 행렬(Orthogonal Matrix)
(5) 대각 행렬(Diagonal Matrix)
6.1.2. 절단된 SVD(Truncated SVD)
6.1.3. 잠재 의미 분석(Latent Semantic Analysis; LSA)
6.1.4. 실습을 통한 이해
(1) 뉴스그룹 데이터에 대한 이해
(2) 텍스트 전처리
(3) TF-IDF 행렬 만들기
(4) 토픽 모델링(Topic Modeling)
6.1.5. LSA의 장단점(Pros and Cons of LSA)
6. 토픽 모델링(Topic Modeling)
토픽(Topic)은 한국어로는 주제라고 한다. 토픽 모델링(Topic Modeling)이란 기계 학습 및 자연어 처리 분야에서 토픽이라는 문서 집합의 추상적인 주제를 발견하기 위한 통계적 모델 중 하나로, 텍스트 본문의 숨겨진 의미 구조를 발견하기 위해 사용되는 텍스트 마이닝 기법이다.
6.1. 잠재 의미 분석(Latent Semantic Analysis; LSA)
LSA는 정확히는 토픽 모델링을 위해 최적화된 알고리즘은 아니지만, 토픽 모델링이라는 분야에 아이디어를 제공한 알고리즘이라고 볼 수 있다. 이에 토픽 모델링 알고리즘인 LDA에 앞서 배워보도록 할 것이다. 뒤에서 배우게 되는 LDA는 LSA의 단점을 개선하여 탄생한 알고리즘으로 토픽 모델링에 보다 적합한 알고리즘이다.
BoW에 기반한 DTM이나 TF-IDF는 기본적으로 단어의 빈도 수를 이용한 수치화 방법이기 때문에 단어의 의미를 고려하지 못한다는 단점이 있었다. (이를 토픽 모델링 관점에서는 단어의 토픽을 고려하지 못한다고도 한다.) 이를 위한 대안으로 DTM의 잠재된(Latent) 의미를 이끌어내는 방법으로 잠재 의미 분석(Latent Semantic Analysis, LSA)이라는 방법이 있다. 이는 때때로 잠재 의미 분석(Latent Semantic Indexing, LSI)라고 불리기도 한다.
이 방법을 이해하기 위해서는 선형대수학의 특이값 분해(Singular Value Decomposition, SVD)를 이해할 필요가 있다. 이 챕터에서는 SVD를 수행하는 구체적인 선형대수학에 대해서는 설명하지 않고, SVD가 갖고있는 의미를 이해하는 것에 초점을 맞춘다.
6.1.1. 특이값 분해(Singular Value Decomposition, SVD)
시작하기에 앞서 여기서는 특이값 분해(Singular Value Decomposition, SVD)는 실수 벡터 공간에 한정하여 내용을 설명함을 명시한다. 즉, SVD란 A가 m x n 행렬일 때, 다음과 같이 3개의 행렬의 곱으로 분해(decomposition)하는 것을 말한다.
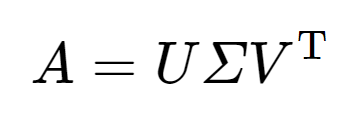
여기서 각 3개의 행렬은 다음과 같은 조건을 만족한다.

여기서 직교행렬(orthogonal matrix)이란 자신과 자신의 전치 행렬(transposed matrix)의 곱 또는 이를 반대로 곱한 결과가 단위행렬(identity matrix)이 되는 행렬을 말한다. 또한 대각행렬(diagonal matrix)이란 주대각선을 제외한 곳의 원소가 모두 0인 행렬을 의미한다.
이때 SVD로 나온 대각행렬의 대각 원소의 값을 행렬 A의 특이값(singular value)라고 한다. 많은 용어가 한꺼번에 나와서 복잡해보이는데 차근 차근 용어를 정리해보도록 하겠다.
(1) 전치 행렬(Transposed Matrix)
전치 행렬(transposed matrix)은 원래의 행렬에서 행과 열을 바꾼 행렬이다. 즉, 주대각선을 축으로 반사 대칭을 하여 얻는 행렬이다. 기호는 기존 행렬 표현의 우측 위에 T를 붙인다. 예를 들어서 기존의 행렬을 M이라고 한다면, 전치 행렬은
아래와 같이 표현한다.
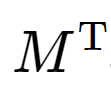

(2) 단위 행렬(Identity Matrix)
단위 행렬(identity matrix)은 주대각선의 원소가 모두 1이며 나머지 원소는 모두 0인 정사각 행렬을 말한다. 보통 줄여서 대문자 I로 표현하기도 하는데, 2 × 2 단위 행렬과 3 × 3 단위 행렬을 표현해보면 다음과 같다.

(3) 역행렬(Inverse Matrix)
단위 행렬(identity matrix)를 이해했다면 역행렬(inverse matrix)을 정의할 수 있다. 만약 행렬 A와 어떤 행렬을 곱했을 때, 결과로서 단위 행렬이 나온다면 이때의 어떤 행렬을 A의 역행렬이라고 하며, A−1라고 표현한다.

(4) 직교 행렬(Orthogonal Matrix)
다시 직교 행렬(orthogonal matrix)의 정의로 돌아가서, 실수 n×n행렬 A에 대해서 A × AT=I를 만족하면서 AT × A=I을 만족하는 행렬 A를 직교 행렬이라고 한다. 그런데 역행렬의 정의를 다시 생각해보면, 결국 직교 행렬은 A−1=AT를 만족한다.
(5) 대각 행렬(Diagonal Matrix)
대각행렬(diagonal matrix)은 주대각선을 제외한 곳의 원소가 모두 0인 행렬을 말한다. 아래의 그림에서는 주대각선의 원소를 a라고 표현하고 있다. 만약 대각 행렬 Σ가 3 × 3 행렬이라면, 다음과 같은 모양을 가진다.
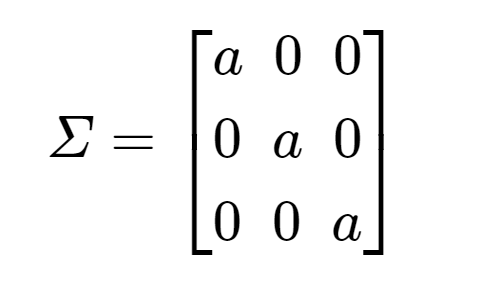
여기까진 정사각행렬이기 때문에 직관적으로 이해가 쉽다. 그런데 정사각행렬이 아니라 직사각행렬이 될 경우를 잘 보아야 헷갈리지 않는다. 만약 행의 크기가 열의 크기보다 크다면 다음과 같은 모양을 가집니다. 즉, m × n 행렬일 때, m > n인 경우를 말한다.

반면 n > m인 경우에는 다음과 같은 모양을 갖는다.

여기까지는 일반적인 대각 행렬에 대한 정의였다. SVD를 통해 나온 대각 행렬 Σ는 추가적인 성질을 가지는데, 대각 행렬 Σ의 주대각원소를 행렬 A의 특이값(singular value)라고 하며, 이를

라고 표현한다고 하였을 때 특이값은 아래와 같이 내림차순으로 정렬된다.

아래의 그림은 특이값 12.4, 9.5, 1.3이 내림차순으로 정렬되어져 있는 모습을 보여준다.

6.1.2. 절단된 SVD (Truncated SVD)
위에서 설명한 SVD를 풀 SVD(full SVD)라고 한다. 하지만 LSA의 경우 풀 SVD에서 나온 3개의 행렬에서 일부 벡터들을 삭제시킨 절단된 SVD(truncated SVD)를 사용하게 된다. 그림을 통해 이해해보도록 하자.

절단된 SVD는 대각 행렬 Σ의 대각 원소의 값 중에서 상위값 t개만 남게 된다. 절단된 SVD를 수행하면 값의 손실이 일어나므로 기존의 행렬 A를 복구할 수 없다. 또한, U행렬과 V행렬의 t열까지만 남긴다. 여기서 t는 우리가 찾고자하는 토픽의 수를 반영한 하이퍼파라미터값이다. 하이퍼파라미터란 사용자가 직접 값을 선택하며 성능에 영향을 주는 매개변수를말한다. 즉, t를 선택하는 것은 쉽지 않은 일이다. t를 크게 잡으면 기존의 행렬 A로부터 다양한 의미를 가져갈 수 있지만, t를 작게 잡아야만 노이즈를 제거할 수 있기 때문이다.
이렇게 일부 벡터들을 삭제하는 것을 데이터의 차원을 줄인다고도 말하는데, 데이터의 차원을 줄이게되면 당연히 풀 SVD를 하였을 때보다 직관적으로 계산 비용이 낮아지는 효과를 얻을 수 있다.
하지만 계산 비용이 낮아지는 것 외에도 상대적으로 중요하지 않은 정보를 삭제하는 효과를 갖고 있는데, 이는 영상 처리 분야에서는 노이즈를 제거한다는 의미를 갖고 자연어 처리 분야에서는 설명력이 낮은 정보를 삭제하고 설명력이 높은 정보를 남긴다는 의미를 갖고 있다. 즉, 다시 말하면 기존의 행렬에서는 드러나지 않았던 심층적인 의미를 확인할 수 있게 해준다.
6.1.3. 잠재 의미 분석(Latent Semantic Analysis, LSA)
기존의 DTM이나 DTM에 단어의 중요도에 따른 가중치를 주었던 TF-IDF 행렬은 단어의 의미를 전혀 고려하지 못한다는 단점을 갖고 있다. LSA는 기본적으로 DTM이나 TF-IDF 행렬에 절단된 SVD(truncated SVD)를 사용하여 차원을 축소시키고, 단어들의 잠재적인 의미를 끌어낸다는 아이디어를 갖고 있다. 실습을 통해 이해해보도록 하자.
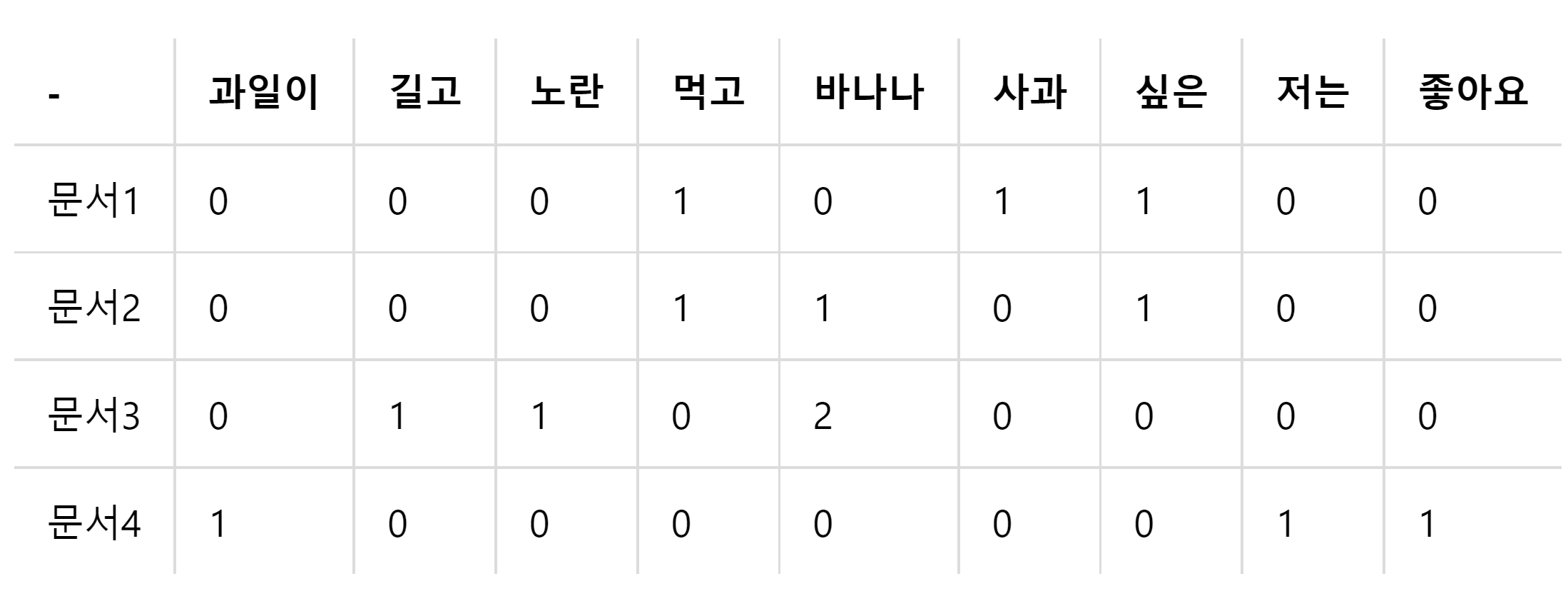
위와 같은 DTM을 실제로 파이썬을 통해서 만들면 다음과 같다.
import numpy as np
A=np.array([[0,0,0,1,0,1,1,0,0],[0,0,0,1,1,0,1,0,0],[0,1,1,0,2,0,0,0,0],[1,0,0,0,0,0,0,1,1]])
np.shape(A)(4, 9)
4 × 9의 크기를 가지는 DTM이 생성되었다. 이에 대해서 풀 SVD(full SVD)를 수행해보겠다. 단, 여기서는 대각 행렬의 변수명을 Σ가 아니라 S를 사용한다. 또한 V의 전치 행렬을 VT라고 하겠다.
U, s, VT = np.linalg.svd(A, full_matrices = True)print(U.round(2))
np.shape(U)
소수점의 길이가 너무 길게 출력하면 보기 힘들어서 두번째 자리까지만 출력하기 위해 .round(2)를 사용한다.
[[-0.24 0.75 0. -0.62]
[-0.51 0.44 -0. 0.74]
[-0.83 -0.49 -0. -0.27]
[-0. -0. 1. 0. ]]
(4, 4)
4 × 4의 크기를 가지는 직교 행렬 U가 생성되었다. 이제 대각 행렬 S를 확인해보자.
print(s.round(2))
np.shape(s)[2.69 2.05 1.73 0.77]
(4,)
Numpy의 linalg.svd()는 특이값 분해의 결과로 대각 행렬이 아니라 특이값의 리스트를 반환한다. 그러므로 앞서 본 수식의 형식으로 보려면 이를 다시 대각 행렬로 바꾸어 주어야 한다. 우선 특이값을 s에 저장하고 대각 행렬 크기의 행렬을 생성한 후에 그 행렬에 특이값을 삽입해보도록 하겠다.
S = np.zeros((4, 9)) # 대각 행렬의 크기인 4 x 9의 임의의 행렬 생성
S[:4, :4] = np.diag(s) # 특이값을 대각행렬에 삽입
print(S.round(2))
np.shape(S)[[2.69 0. 0. 0. 0. 0. 0. 0. 0. ]
[0. 2.05 0. 0. 0. 0. 0. 0. 0. ]
[0. 0. 1.73 0. 0. 0. 0. 0. 0. ]
[0. 0. 0. 0.77 0. 0. 0. 0. 0. ]]
(4, 9)
4 × 9의 크기를 가지는 대각 행렬 S가 생성되었다. 2.69 > 2.05 > 1.73 > 0.77 순으로 값이 내림차순을 보이는 것을 확인할 수 있다.
print(VT.round(2))
np.shape(VT)[[-0. -0.31 -0.31 -0.28 -0.8 -0.09 -0.28 -0. -0. ]
[ 0. -0.24 -0.24 0.58 -0.26 0.37 0.58 -0. -0. ]
[ 0.58 -0. 0. 0. -0. 0. -0. 0.58 0.58]
[ 0. -0.35 -0.35 0.16 0.25 -0.8 0.16 -0. -0. ]
[-0. -0.78 -0.01 -0.2 0.4 0.4 -0.2 0. 0. ]
[-0.29 0.31 -0.78 -0.24 0.23 0.23 0.01 0.14 0.14]
[-0.29 -0.1 0.26 -0.59 -0.08 -0.08 0.66 0.14 0.14]
[-0.5 -0.06 0.15 0.24 -0.05 -0.05 -0.19 0.75 -0.25]
[-0.5 -0.06 0.15 0.24 -0.05 -0.05 -0.19 -0.25 0.75]]
(9, 9)
9 × 9의 크기를 가지는 직교 행렬 VT(V의 전치 행렬)가 생성되었다. 즉, U × S × VT를 하면 기존의 행렬 A가 나와야 한다. Numpy의 allclose()는 2개의 행렬이 동일하면 True를 리턴한다. 이를 사용하여 정말로 기존의 행렬 A와 동일한지 확인해보겠다.
np.allclose(A, np.dot(np.dot(U,S), VT).round(2))True
지금까지 수행한 것은 풀 SVD(Full SVD)이다. 이제 t를 정하고, 절단된 SVD(Truncated SVD)를 수행해보도록 하자. 여기서는 t=2로 하겠다. 우선 대각 행렬 S 내의 특이값 중에서 상위 2개만 남기고 제거해보도록 하자.
S=S[:2,:2]
print(S.round(2))[[2.69 0. ]
[0. 2.05]]
상위 2개의 값만 남기고 나머지는 모두 제거된 것을 볼 수 있다. 이제 직교 행렬 U에 대해서도 2개의 열만 남기고 제거한다.
U=U[:,:2]
print(U.round(2))[[-0.24 0.75]
[-0.51 0.44]
[-0.83 -0.49]
[-0. -0. ]]
2개의 열만 남기고 모두 제거가 된 것을 볼 수 있다. 이제 행렬 V의 전치 행렬인 VT에 대해서 2개의 행만 남기고 제거한다. 이는 V관점에서는 2개의 열만 남기고 제거한 것이 된다.
VT=VT[:2,:]
print(VT.round(2))[[-0. -0.31 -0.31 -0.28 -0.8 -0.09 -0.28 -0. -0. ]
[0. -0.24 -0.24 0.58 -0.26 0.37 0.58 -0. -0. ]]
이제 축소된 행렬 U, S, VT에 대해서 다시 U × S × VT연산을 하면 기존의 A와는 다른 결과가 나오게 된다. 값이 손실되었기 때문에 이 세 개의 행렬로는 이제 기존의 A행렬을 복구할 수 없다. U × S × VT연산을 해서 나오는 값을 A_prime이라 하고 기존의 행렬 A와 값을 비교해보도록 하겠다.
A_prime=np.dot(np.dot(U,S), VT)
print(A)
print(A_prime.round(2))[[0 0 0 1 0 1 1 0 0]
[0 0 0 1 1 0 1 0 0]
[0 1 1 0 2 0 0 0 0]
[1 0 0 0 0 0 0 1 1]]
[[0. -0.17 -0.17 1.08 0.12 0.62 1.08 -0. -0. ]
[0. 0.2 0.2 0.91 0.86 0.45 0.91 0. 0. ]
[0. 0.93 0.93 0.03 2.05 -0.17 0.03 0. 0. ]
[0. 0. 0. 0. 0. 0. 0. 0. 0. ]]
대체적으로 기존에 0인 값들은 0에 가끼운 값이 나오고, 1인 값들은 1에 가까운 값이 나오는 것을 볼 수 있다. 또한 값이 제대로 복구되지 않은 구간도 존재해보인다. 이제 이렇게 차원이 축소된 U, S, VT의 크기가 어떤 의미를 가지고 있는지 알아보자.
축소된 U는 4 × 2의 크기를 가지는데, 이는 잘 생각해보면 문서의 개수 × 토픽의 수 t의 크기이다. 단어의 개수인 9는 유지되지 않는데 문서의 개수인 4의 크기가 유지되었으니 4개의 문서 각각을 2개의 값으로 표현하고 있다. 즉, U의 각 행은 잠재 의미를 표현하기 위한 수치화 된 각각의 문서 벡터라고 볼 수 있다. 축소된 VT는 2 × 9의 크기를 가지는데, 이는 잘 생각해보면 토픽의 수 t × 단어의 개수의 크기이다. VT의 각 열은 잠재 의미를 표현하기 위해 수치화된 각각의 단어 벡터라고 볼 수 있다.
이 문서 벡터들과 단어 벡터들을 통해 다른 문서의 유사도, 다른 단어의 유사도, 단어(쿼리)로부터 문서의 유사도를 구하는 것들이 가능해진다.
6.1.4. 실습을 통한 이해
사이킷런에서는 Twenty Newsgroups이라고 불리는 20개의 다른 주제를 가진 뉴스그룹 데이터를 제공한다. 앞서 언급했듯이 LSA가 토픽 모델링에 최적화 된 알고리즘은 아니지만, 토픽 모델링이라는 분야의 시초가 되는 알고리즘이다. 여기서는 LSA를 사용해서 문서의 수를 원하는 토픽의 수로 압축한 뒤에 각 토픽 당 가장 중요한 단어 5개를 출력하는 실습으로 토픽 모델링을 수행한다.
- 뉴스그룹 데이터는 뉴스 데이터가 아니다.
1) 뉴스그룹 데이터에 대한 이해
import pandas as pd
from sklearn.datasets import fetch_20newsgroups
dataset = fetch_20newsgroups(shuffle=True, random_state=1, remove=('headers', 'footers', 'quotes'))
documents = dataset.data
len(documents)11314
훈련에 사용할 뉴스그룹 데이터는 총 11,314개이다. 이 중 첫번째 훈련용 샘플을 출력해보겠다.
documents[1]"\n\n\n\n\n\n\nYeah, do you expect people to read the FAQ, etc. and actually accept hard\natheism? No, you need a little leap of faith, Jimmy. Your logic runs out\nof steam! \n\n\n\n\n\n\n\n
Jim,\n\nSorry I can't pity you, Jim. And I'm sorry that you have these feelings of\ndenial about the faith you need to get by. Oh well, just pretend that it will\nall end happily ever after anyway. Maybe if you start a new newsgroup,\nalt.atheist.hard, you won't be bummin' so much?\n\n\n\n\n\n\nBye-Bye, Big Jim. Don't forget your Flintstone's Chewables! :) \n--\nBake Timmons, III"
뉴스그룹 데이터에는 특수문자가 포함된 다수의 영어문장으로 구성되어져 있다. 이런 형식의 샘플이 총 11,314개 존재한다. 사이킷런이 제공하는 뉴스그룹 데이터에서 target_name에는 본래 이 뉴스그룹 데이터가 어떤 20개의 카테고리를 갖고있었는지가 저장되어져 있다. 이를 출력해보겠다.
print(dataset.target_names)['alt.atheism', 'comp.graphics', 'comp.os.ms-windows.misc', 'comp.sys.ibm.pc.hardware', 'comp.sys.mac.hardware', 'comp.windows.x', 'misc.forsale', 'rec.autos', 'rec.motorcycles', 'rec.sport.baseball', 'rec.sport.hockey', 'sci.crypt', 'sci.electronics', 'sci.med', 'sci.space', 'soc.religion.christian', 'talk.politics.guns', 'talk.politics.mideast', 'talk.politics.misc', 'talk.religion.misc']
2) 텍스트 전처리
시작하기 앞서, 텍스트 데이터에 대해서 가능한한 정제 과정을 거쳐야만 한다. 기본적인 아이디어는 알파벳을 제외한 구두점, 숫자, 특수 문자를 제거하는 것이다. 이는 텍스트 전처리 챕터에서 정제 기법으로 배웠던 정규 표현식을 통해서 해결할 수 있다. 또한 짧은 단어는 유용한 정보를 담고있지 않다고 가정하고, 길이가 짧은 단어도 제거한다. 그리고 마지막으로 모든 알파벳을 소문자로 바꿔서 단어의 개수를 줄이는 작업을 한다.
news_df = pd.DataFrame({'document':documents})
# 특수 문자 제거
news_df['clean_doc'] = news_df['document'].str.replace("[^a-zA-Z]", " ")
# 길이가 3이하인 단어는 제거 (길이가 짧은 단어 제거)
news_df['clean_doc'] = news_df['clean_doc'].apply(lambda x: ' '.join([w for w in x.split() if len(w)>3]))
# 전체 단어에 대한 소문자 변환
news_df['clean_doc'] = news_df['clean_doc'].apply(lambda x: x.lower())
데이터의 정제가 끝났다. 다시 첫번째 훈련용 뉴스그룹 샘플만 출력하여 정제 전, 후에 어떤 차이가 있는지 확인해보겠다.
news_df['clean_doc'][1]'yeah expect people read actually accept hard atheism need little leap faith jimmy your logic runs steam sorry pity sorry that have these feelings denial about faith need well just pret
end that will happily ever after anyway maybe start newsgroup atheist hard bummin much forget your flintstone chewables bake timmons'
우선 특수문자가 제거되었으며, if나 you와 같은 길이가 3이하인 단어가 제거된 것을 확인할 수 있다. 뿐만 아니라 대문자가 전부 소문자로 바뀌었다. 이제 뉴스그룹 데이터에서 불용어를 제거한다. 불용어를 제거하기 위해서 토큰화를 우선 수행한다. 토큰화와 불용어 제거를 순차적으로 진행한다.
from nltk.corpus import stopwords
stop_words = stopwords.words('english') # NLTK로부터 불용어를 받아옵니다.
tokenized_doc = news_df['clean_doc'].apply(lambda x: x.split()) # 토큰화
tokenized_doc = tokenized_doc.apply(lambda x: [item for item in x if item not in stop_words])
# 불용어를 제거합니다.
다시 첫번째 훈련용 뉴스그룹 샘플을 출력한다.
print(tokenized_doc[1])['yeah', 'expect', 'people', 'read', 'actually', 'accept', 'hard', 'atheism', 'need', 'little', 'leap', 'faith', 'jimmy', 'logic', 'runs', 'steam', 'sorry', 'pity', 'sorry', 'feelings', 'denial', 'faith', 'need', 'well', 'pretend', 'happily', 'ever', 'anyway', 'maybe', 'start', 'newsgroup', 'atheist', 'hard', 'bummin', 'much', 'forget', 'flintstone', 'chewables', 'bake', 'timmons']
기존에 있었던 불용어에 속하던 your, about, just, that, will, after 단어들이 사라졌을 뿐만 아니라, 토큰화가 수행된 것을 확인할 수 있다.
3) TF-IDF 행렬 만들기
불용어 제거를 위해 토큰화 작업을 수행하였지만, TfidfVectorizer(TF-IDF 챕터 참고)는 기본적으로 토큰화가 되어있지 않은 텍스트 데이터를 입력으로 사용한다. 그렇기 때문에 TfidfVectorizer를 사용해서 TF-IDF 행렬을 만들기 위해서 다시 토큰화 작업을 역으로 취소하는 작업을 수행해보도록 하겠다. 이를 역토큰화(Detokenization)라고 한다.
# 역토큰화 (토큰화 작업을 역으로 되돌림)
detokenized_doc = []
for i in range(len(news_df)):
t = ' '.join(tokenized_doc[i])
detokenized_doc.append(t)
news_df['clean_doc'] = detokenized_doc
역토큰화가 제대로 되었는지 다시 첫번째 훈련용 뉴스그룹 샘플을 출력하여 확인해보겠다.
news_df['clean_doc'][1]'yeah expect people read actually accept hard atheism need little leap faith jimmy logic runs steam sorry pity sorry feelings denial faith need well pretend happily ever anyway maybe start newsgroup atheist hard bummin much forget flintstone chewables bake timmons'
정상적으로 불용어가 제거된 상태에서 역토큰화가 수행되었음을 확인할 수 있다.
이제 사이킷런의 TfidfVectorizer를 통해 단어 1,000개에 대한 TF-IDF 행렬을 만들 것이다. 물론 텍스트 데이터에 있는 모든 단어를 가지고 행렬을 만들 수는 있겠지만, 여기서는 1,000개의 단어로 제한하도록 하겠다.
from sklearn.feature_extraction.text import TfidfVectorizer
vectorizer = TfidfVectorizer(stop_words='english',
max_features= 1000, # 상위 1,000개의 단어만 보존
max_df = 0.5,
smooth_idf=True)
X = vectorizer.fit_transform(news_df['clean_doc'])
X.shape # TF-IDF 행렬의 크기 확인(11314, 1000)
11,314 × 1,000의 크기를 가진 TF-IDF 행렬이 생성되었음을 확인할 수 있다.
4) 토픽 모델링(Topic Modeling)
이제 TF-IDF 행렬을 다수의 행렬로 분해해보도록 하겠다. 여기서는 사이킷런의 절단된 SVD(Truncated SVD)를 사용한다. 절단된 SVD를 사용하면 차원을 축소할 수 있다. 원래 기존 뉴스그룹 데이터가 20개의 카테고리를 갖고 있었기 때문에, 20개의 토픽을 가졌다고 가정하고 토픽 모델링을 시도해보겠다. 토픽의 숫자는 n_components의 파라미터로 지정이 가능하다.
from sklearn.decomposition import TruncatedSVD
svd_model = TruncatedSVD(n_components=20, algorithm='randomized', n_iter=100, random_state=122)
svd_model.fit(X)
len(svd_model.components_)20
여기서 svd_model.componets_는 앞서 배운 LSA에서 VT에 해당된다.
np.shape(svd_model.components_)(20, 1000)
정확하게 토픽의 수 t × 단어의 수의 크기를 가지는 것을 볼 수 있다.
terms = vectorizer.get_feature_names() # 단어 집합. 1,000개의 단어가 저장됨.
def get_topics(components, feature_names, n=5):
for idx, topic in enumerate(components):
print("Topic %d:" % (idx+1), [(feature_names[i], topic[i].round(5)) for i in topic.argsort()[:-n - 1:-1]])
get_topics(svd_model.components_,terms)
각 20개의 행의 각 1,000개의 열 중 가장 값이 큰 5개의 값을 찾아서 단어로 출력한다.
Topic 1: [('like', 0.2138), ('know', 0.20031), ('people', 0.19334), ('think', 0.17802), ('good', 0.15105)]
Topic 2: [('thanks', 0.32918), ('windows', 0.29093), ('card', 0.18016), ('drive', 0.1739), ('mail', 0.15131)]
Topic 3: [('game', 0.37159), ('team', 0.32533), ('year', 0.28205), ('games', 0.25416), ('season', 0.18464)]
Topic 4: [('drive', 0.52823), ('scsi', 0.20043), ('disk', 0.15518), ('hard', 0.15511), ('card', 0.14049)]
Topic 5: [('windows', 0.40544), ('file', 0.25619), ('window', 0.1806), ('files', 0.16196), ('program', 0.14009)]
Topic 6: [('government', 0.16085), ('chip', 0.16071), ('mail', 0.15626), ('space', 0.15047), ('information', 0.13582)]
Topic 7: [('like', 0.67121), ('bike', 0.14274), ('know', 0.11189), ('chip', 0.11043), ('sounds', 0.10389)]
Topic 8: [('card', 0.44948), ('sale', 0.21639), ('video', 0.21318), ('offer', 0.14896), ('monitor', 0.1487)]
Topic 9: [('know', 0.44869), ('card', 0.35699), ('chip', 0.17169), ('video', 0.15289), ('government', 0.15069)]
Topic 10: [('good', 0.41575), ('know', 0.23137), ('time', 0.18933), ('bike', 0.11317), ('jesus', 0.09421)]
Topic 11: [('think', 0.7832), ('chip', 0.10776), ('good', 0.10613), ('thanks', 0.08985), ('clipper', 0.07882)]
Topic 12: [('thanks', 0.37279), ('right', 0.21787), ('problem', 0.2172), ('good', 0.21405), ('bike', 0.2116)]
Topic 13: [('good', 0.36691), ('people', 0.33814), ('windows', 0.28286), ('know', 0.25238), ('file', 0.18193)]
Topic 14: [('space', 0.39894), ('think', 0.23279), ('know', 0.17956), ('nasa', 0.15218), ('problem', 0.12924)]
Topic 15: [('space', 0.3092), ('good', 0.30207), ('card', 0.21615), ('people', 0.20208), ('time', 0.15716)]
Topic 16: [('people', 0.46951), ('problem', 0.20879), ('window', 0.16), ('time', 0.13873), ('game', 0.13616)]
Topic 17: [('time', 0.3419), ('bike', 0.26896), ('right', 0.26208), ('windows', 0.19632), ('file', 0.19145)]
Topic 18: [('time', 0.60079), ('problem', 0.15209), ('file', 0.13856), ('think', 0.13025), ('israel', 0.10728)]
Topic 19: [('file', 0.4489), ('need', 0.25951), ('card', 0.1876), ('files', 0.17632), ('problem', 0.1491)]
Topic 20: [('problem', 0.32797), ('file', 0.26268), ('thanks', 0.23414), ('used', 0.19339), ('space', 0.13861)]
5) LSA의 장단점(Pros and Cons of LSA)
정리해보면 LSA는 쉽고 빠르게 구현이 가능할 뿐만 아니라 단어의 잠재적인 의미를 이끌어낼 수 있어 문서의 유사도 계산 등에서 좋은 성능을 보여준다는 장점을 갖고 있다. 하지만 SVD의 특성상 이미 계산된 LSA에 새로운 데이터를 추가하여 계산하려고하면 보통 처음부터 다시 계산해야 한다. 즉, 새로운 정보에 대해 업데이트가 어렵다. 이는 최근 LSA 대신 Word2Vec 등 단어의 의미를 벡터화할 수 있는 또 다른 방법론인 인공 신경망 기반의 방법론이 각광받는 이유이기도 하다.




