| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- 파이썬기초100제
- 파이썬
- GenAI
- 리트코드
- 파이썬알고리즘
- codeup
- gcp
- C#
- Azure
- 빅데이터
- nlp
- Blazor
- 파이썬기초
- TwoPointer
- 생성형AI
- 구글퀵랩
- GenerativeAI
- Python3
- LeetCode
- Python
- Microsoft
- 데이터사이언스
- 알고리즘
- 코드업
- 머신러닝
- 클라우드
- 자연어처리
- 릿코드
- 코드업파이썬
- 투포인터
- Today
- Total
Tech for good
[딥러닝을 이용한 자연어 처리 입문] 5. 벡터의 유사도(Vector Similarity) - 2. 여러가지 유사도 기법 본문
[딥러닝을 이용한 자연어 처리 입문] 5. 벡터의 유사도(Vector Similarity) - 2. 여러가지 유사도 기법
Diana Kang 2021. 10. 20. 08:57목차
5. 벡터의 유사도(Vector Similarity)
5.2. 여러가지 유사도 기법
5.2.1. 유클리드 거리(Euclidean distance)
5.2.2. 자카드 유사도(Jaccard similarity)
5. 벡터의 유사도(Vector Similarity)
5.2. 여러가지 유사도 기법
문서의 유사도를 구하기 위한 방법으로는 코사인 유사도 외에도 여러가지 방법들이 있다. 여기서는 문서의 유사도를 구할 수 있는 다른 방법들을 학습한다.
5.1.1. 유클리드 거리(Euclideam distance)
유클리드 거리(euclidean distance)는 문서의 유사도를 구할 때 자카드 유사도나 코사인 유사도만큼, 유용한 방법은 아니다. 하지만 여러 가지 방법을 이해하고, 시도해보는 것 자체만으로 다른 개념들을 이해할 때 도움이 되므로 의미가 있다.
다차원 공간에서 두개의 점 p와 q가 각각 p=(p1,p2,p3,...,pn)과 q=(q1,q2,q3,...,qn)의 좌표를 가질 때 두 점 사이의 거리를 계산하는 유클리드 거리 공식은 다음과 같다.
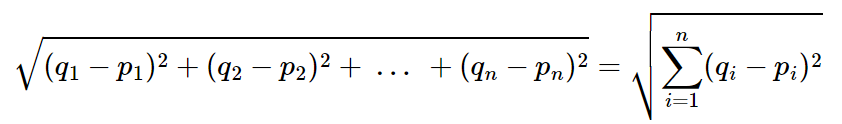
다차원 공간이라고 가정하면 처음 보는 입장에서는 식이 너무 복잡해보인다. 좀 더 쉽게 이해하기 위해서 2차원 공간이라고 가정하고 두 점 사이의 거리를 좌표 평면 상에서 시각화해보겠다.

2차원 좌표 평면 상에서 두 점 p와 q사이의 직선 거리를 구하는 문제이다. 위의 경우에는 직각 삼각형으로 표현이 가능하므로, 중학교 수학 과정인 피타고라스의 정리를 통해 p와 q 사이의 거리를 계산할 수 있다. 즉, 2차원 좌표 평면에서 두 점 사이의 유클리드 거리 공식은 피타고라스의 정리를 통해 두 점 사이의 거리를 구하는 것과 동일하다.
다시 원점으로 돌아가서 여러 문서에 대해서 유사도를 구하고자 유클리드 거리 공식을 사용한다는 것은, 앞서 본 2차원을 단어의 총 개수만큼의 차원으로 확장하는 것과 같다. 예를 들어 아래와 같은 DTM이 있다고 가정해보자.

단어의 개수가 4개이므로 이는 4차원 공간에 문서1, 문서2, 문서3을 배치하는 것과 같다. 이때 다음과 같은 문서Q에 대해서 문서1, 문서2, 문서3 중 가장 유사한 문서를 찾아내고자 한다.

이때 유클리드 거리를 통해 유사도를 구하려고 한다면, 문서Q 또한 다른 문서들처럼 4차원 공간에 배치시켰다는 관점에서 4차원 공간에서의 각각의 문서들과의 유클리드 거리를 구하면 된다. 이를 파이썬 코드로 구현해보겠다.
import numpy as np
def dist(x,y):
return np.sqrt(np.sum((x-y)**2))
doc1 = np.array((2,3,0,1))
doc2 = np.array((1,2,3,1))
doc3 = np.array((2,1,2,2))
docQ = np.array((1,1,0,1))
print(dist(doc1,docQ))
print(dist(doc2,docQ))
print(dist(doc3,docQ))2.23606797749979
3.1622776601683795
2.449489742783178
유클리드 거리의 값이 가장 작다는 것은 문서 간의 거리가 가장 가깝다는 것을 의미한다. 즉, 문서1이 문서Q와 가장 유사하다고 볼 수 있다.
5.2.2. 자카드 유사도(Jaccard similartiy)
A와 B 두 개의 집합이 있다고 해보자. 이때 교집합은 두 개의 집합에서 공통으로 가지고 있는 원소들의 집합을 말한다. 즉, 합집합에서 교집합의 비율을 구한다면 두 집합 A와 B의 유사도를 구할 수 있다는 것이 자카드 유사도(jaccard similarity)의 아이디어이다. 자카드 유사도는 0과 1사이의 값을 가지며, 만약 두 집합이 동일하다면 1의 값을 가지고, 두 집합의 공통 원소가 없다면 0의 값을 갖는다. 자카드 유사도를 구하는 함수를 J라고 하였을 때, 자카드 유사도 함수 J는 아래와 같다.

두 개의 비교할 문서를 각각 doc1, doc2라고 했을 때 doc1과 doc2의 문서의 유사도를 구하기 위한 자카드 유사도는 이와 같다.

즉, 두 문서 doc1, doc2 사이의 자카드 유사도 J(doc1,doc2)는 두 집합의 교집합 크기를 두 집합의 합집합 크기로 나눈 값으로 정의된다. 간단한 예를 통해서 이해해보겠다.
doc1 = "apple banana everyone like likey watch card holder"
doc2 = "apple banana coupon passport love you"
# 토큰화
tokenized_doc1 = doc1.split()
tokenized_doc2 = doc2.split()
# 토큰화 결과 출력
print(tokenized_doc1)
print(tokenized_doc2)['apple', 'banana', 'everyone', 'like', 'likey', 'watch', 'card', 'holder']
['apple', 'banana', 'coupon', 'passport', 'love', 'you']
이 때 문서1과 문서2의 합집합을 구해보겠다.
union = set(tokenized_doc1).union(set(tokenized_doc2))
print(union){'card', 'holder', 'passport', 'banana', 'apple', 'love', 'you', 'likey', 'coupon', 'like', 'watch', 'everyone'}
문서1과 문서2의 합집합의 단어의 총 개수는 12개인 것을 확인할 수 있다. 그렇다면, 문서1과 문서2의 교집합을 구해보겠다. 즉, 문서1과 문서2에서 둘 다 등장한 단어를 구하는 것이다.
intersection = set(tokenized_doc1).intersection(set(tokenized_doc2))
print(intersection){'banana', 'apple'}
문서1과 문서2에서 둘 다 등장한 단어는 banana와 apple 총 2개이다. 이제 교집합의 수를 합집합의 수로 나누면 자카드 유사도가 계산된다.
print(len(intersection)/len(union))0.16666666666666666
'IT > Data Science' 카테고리의 다른 글
| [파이썬 정규표현식] re.sub() (0) | 2021.10.29 |
|---|---|
| .iteritems() 함수 (0) | 2021.10.29 |
| [딥러닝을 이용한 자연어 처리 입문] 5. 벡터의 유사도(Vector Similarity) - 1. 코사인 유사도(Cosine Similarity) (0) | 2021.10.20 |
| [Elasticsearch] Elastic Cloud에서 Nori Tokenizer 설치하기 (Extensions 활용) (0) | 2021.10.19 |
| [딥러닝을 이용한 자연어 처리 입문] 6. 토픽 모델링(Topic Modeling)- 3) 잠재 디리클레 할당(LDA) 실습2 (2) | 2021.10.14 |



